共通テスト 数学II・数学B・数学C 2025年度 第1問 解説
【必答問題】
問題編
問題
(1) $0 \leqq \theta \lt \pi$ のとき、方程式\[ \sin\left(\theta + \frac{\pi}{6}\right) = \sin 2\theta \quad \cdots \text{①} \]の解を求めよう。以下では、$\alpha = \theta + \dfrac{\pi}{6}$ 、$\beta = 2\theta$ とおく。このとき、① は\[ \sin \alpha = \sin \beta \quad \cdots \text{②} \]となる。
(i) 二つの一般角 $\alpha$ と $\beta$ が等しければ、$\sin \alpha$ と $\sin \beta$ は等しい。$\alpha = \beta$ を満たす $\theta$ は $\dfrac{\pi}{\myBox{ア}}$ であり、これは ① の解の一つである。そして、$\theta = \dfrac{\pi}{\mybox{ア}}$ のとき\[ \sin\left(\theta + \frac{\pi}{6}\right) = \sin 2\theta = \frac{\sqrt{\myBox{イ}}}{\myBox{ウ}} \]となる。
(ii) 太郎さんと花子さんは、$\theta = \dfrac{\pi}{\mybox{ア}}$ 以外の ① の解を求める方法について話している。
- 角が等しくなくても、サインの値が等しくなることがあるね。
- サインの値が等しくなるのはどんなときか、単位円を用いて考えてみようか。
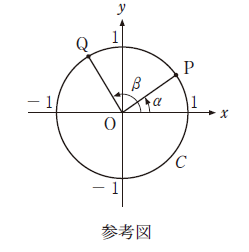
$\mathrm{O}$ を原点とする座標平面において、中心が $\mathrm{O}$ で、半径が $1$ の円を $C$ とする。さらに、$\alpha$ の動径と $C$ との交点を $\mathrm{P}$、$\beta$ の動径と $C$ との交点を $\mathrm{Q}$ とする。ここで、動径は $\mathrm{O}$ を中心とし、その始線は $x$ 軸の正の部分とする。
② が成り立つときに、点 $\mathrm{P}$ と点 $\mathrm{Q}$ の間につねに成り立つ関係の記述として、次の 0 ~ 3 のうち、正しいものは $\dBox{エ}$ である。
$\dBox{エ}$ の解答群
0: 点 $\mathrm{P}$ と点 $\mathrm{Q}$ は同じ点である。
1: 点 $\mathrm{P}$ の $x$ 座標と、点 $\mathrm{Q}$ の $x$ 座標が等しい。
2: 点 $\mathrm{P}$ の $y$ 座標と、点 $\mathrm{Q}$ の $y$ 座標が等しい。
3: 点 $\mathrm{P}$ と点 $\mathrm{Q}$ は、原点 $\mathrm{O}$ に関して対称である。(iii) $\theta \neq \dfrac{\pi}{\mybox{ア}}$ とする。
・ $0 \leqq \theta \leqq \dfrac{\pi}{2}$ の場合を考える。このとき、$0 \leqq \beta \leqq \pi$ であるので、② が成り立つとき、(ii) で考察したことに注意すると、$\alpha$ と $\beta$ は
\[ \alpha + \beta = \dBox{オ} \]を満たすことがわかる。これより、$0 \leqq \theta \leqq \dfrac{\pi}{2}$ のときの ① の解
\[ \theta = \frac{\myBox{カ}}{\myBox{キク}}\pi \]を得る。・ $\dfrac{\pi}{2} \lt \theta \lt \pi$ の場合を考える。このとき、$\pi \lt \beta \lt 2\pi$ であるので、② が成り立つとき、(ii) で考察したことに注意すると、$\alpha$ と $\beta$ は
\[ \alpha + \beta = \dBox{ケ} \]
を満たすことがわかる。これより、$\dfrac{\pi}{2} \lt \theta \lt \pi$ のときの ① の解
\[ \theta = \frac{\myBox{コサ}}{\myBox{シス}}\pi \]を得る。以上より、$0 \leqq \theta \lt \pi$ のとき、① の解は
\[ \theta = \frac{\pi}{\mybox{ア}} , \frac{\mybox{カ}}{\mybox{キク}}\pi, \frac{\mybox{コサ}}{\mybox{シス}}\pi \]である。$\dbox{オ},$ $\dbox{ケ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $0$
1: $\dfrac{\pi}{2}$
2: $\pi$
3: $\dfrac{3}{2}\pi$
4: $2\pi$
5: $\dfrac{5}{2}\pi$
6: $3\pi$
7: $\dfrac{7}{2}\pi$
(2) $0 \leqq \theta \lt \pi$ のとき、方程式
\[ \cos\left(\theta + \frac{\pi}{6}\right) = \cos 2\theta \]の解は
\[ \theta = \frac{\pi}{\myBox{セ}} , \frac{\myBox{ソタ}}{\myBox{チツ}}\pi \]である。
考え方
三角関数を使って書かれた等式を、単位円を使って解く問題です。誘導が細かくついているので、それに従って解いていきます。
$\alpha+\beta$ は、図をかいて、対称性を利用して求めます。(2)もほぼ同じです。 $\sin$ と $\cos$ で何が違うかを考えて、同じように解きましょう。
【必答問題】
解答編
問題
(1) $0 \leqq \theta \lt \pi$ のとき、方程式\[ \sin\left(\theta + \frac{\pi}{6}\right) = \sin 2\theta \quad \cdots \text{①} \]の解を求めよう。以下では、$\alpha = \theta + \dfrac{\pi}{6}$ 、$\beta = 2\theta$ とおく。このとき、① は\[ \sin \alpha = \sin \beta \quad \cdots \text{②} \]となる。
(i) 二つの一般角 $\alpha$ と $\beta$ が等しければ、$\sin \alpha$ と $\sin \beta$ は等しい。$\alpha = \beta$ を満たす $\theta$ は $\dfrac{\pi}{\myBox{ア}}$ であり、これは ① の解の一つである。そして、$\theta = \dfrac{\pi}{\mybox{ア}}$ のとき\[ \sin\left(\theta + \frac{\pi}{6}\right) = \sin 2\theta = \frac{\sqrt{\myBox{イ}}}{\myBox{ウ}} \]となる。
解説
(1)
(i)
$\theta+\dfrac{\pi}{6}=2\theta$ より、 $\theta=\dfrac{\pi}{6}$ です。このとき、\[ \sin2\theta=\sin\frac{\pi}{3}=\frac{\sqrt{3}}{2} \]となります。
解答
ア:6
イウ:32
解答編 つづき
問題
(ii) 太郎さんと花子さんは、$\theta = \dfrac{\pi}{\mybox{ア}}$ 以外の ① の解を求める方法について話している。
- 角が等しくなくても、サインの値が等しくなることがあるね。
- サインの値が等しくなるのはどんなときか、単位円を用いて考えてみようか。
$\mathrm{O}$ を原点とする座標平面において、中心が $\mathrm{O}$ で、半径が $1$ の円を $C$ とする。さらに、$\alpha$ の動径と $C$ との交点を $\mathrm{P}$、$\beta$ の動径と $C$ との交点を $\mathrm{Q}$ とする。ここで、動径は $\mathrm{O}$ を中心とし、その始線は $x$ 軸の正の部分とする。
② が成り立つときに、点 $\mathrm{P}$ と点 $\mathrm{Q}$ の間につねに成り立つ関係の記述として、次の 0 ~ 3 のうち、正しいものは $\dBox{エ}$ である。
$\dBox{エ}$ の解答群
0: 点 $\mathrm{P}$ と点 $\mathrm{Q}$ は同じ点である。
1: 点 $\mathrm{P}$ の $x$ 座標と、点 $\mathrm{Q}$ の $x$ 座標が等しい。
2: 点 $\mathrm{P}$ の $y$ 座標と、点 $\mathrm{Q}$ の $y$ 座標が等しい。
3: 点 $\mathrm{P}$ と点 $\mathrm{Q}$ は、原点 $\mathrm{O}$ に関して対称である。
解説
(1)
(ii)
$\sin$ は $y$ 座標を表しているので、$\sin\alpha=\sin\beta$ が成り立つのは、 $\mathrm{P,Q}$ の $y$ 座標が等しいときです。
解答
エ:2
解答編 つづき
問題
(iii) $\theta \neq \dfrac{\pi}{\mybox{ア}}$ とする。
・ $0 \leqq \theta \leqq \dfrac{\pi}{2}$ の場合を考える。このとき、$0 \leqq \beta \leqq \pi$ であるので、② が成り立つとき、(ii) で考察したことに注意すると、$\alpha$ と $\beta$ は
\[ \alpha + \beta = \dBox{オ} \]を満たすことがわかる。これより、$0 \leqq \theta \leqq \dfrac{\pi}{2}$ のときの ① の解
\[ \theta = \frac{\myBox{カ}}{\myBox{キク}}\pi \]を得る。・ $\dfrac{\pi}{2} \lt \theta \lt \pi$ の場合を考える。このとき、$\pi \lt \beta \lt 2\pi$ であるので、② が成り立つとき、(ii) で考察したことに注意すると、$\alpha$ と $\beta$ は
\[ \alpha + \beta = \dBox{ケ} \]
を満たすことがわかる。これより、$\dfrac{\pi}{2} \lt \theta \lt \pi$ のときの ① の解
\[ \theta = \frac{\myBox{コサ}}{\myBox{シス}}\pi \]を得る。以上より、$0 \leqq \theta \lt \pi$ のとき、① の解は
\[ \theta = \frac{\pi}{\mybox{ア}} , \frac{\mybox{カ}}{\mybox{キク}}\pi, \frac{\mybox{コサ}}{\mybox{シス}}\pi \]である。$\dbox{オ},$ $\dbox{ケ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $0$
1: $\dfrac{\pi}{2}$
2: $\pi$
3: $\dfrac{3}{2}\pi$
4: $2\pi$
5: $\dfrac{5}{2}\pi$
6: $3\pi$
7: $\dfrac{7}{2}\pi$
解説
(1)
(iii)
$0\leqq \theta\leqq \dfrac{\pi}{2}$ のときを考えます。
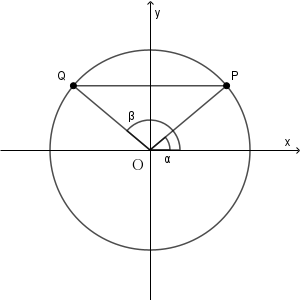
$\mathrm{P,Q}$ の $y$ 座標が等しいので、 $y$ 軸を中心にして左右対称です。2つの角の中間は $\dfrac{\pi}{2}$ 、つまり、2つの角の平均が $\dfrac{\pi}{2}$ なので、 $\alpha+\beta=\pi$ が成り立ちます。よって
\begin{eqnarray}
\theta+\frac{\pi}{6} +2\theta &=& \pi \\[5pt]
3\theta &=& \frac{5\pi}{6} \\[5pt]
\theta &=& \frac{5}{18}\pi \\[5pt]
\end{eqnarray}となります。
次に、$\dfrac{\pi}{2} \lt \theta\lt \pi$ のときを考えます。
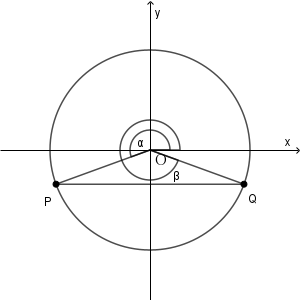
$\mathrm{P,Q}$ の $y$ 座標が等しいので、この場合も左右対称です。2つの角の平均は $\dfrac{3}{2}\pi$ だから、\[ \alpha+\beta=3\pi \]が成り立ちます。よって
\begin{eqnarray}
\theta+\frac{\pi}{6} +2\theta &=& 3\pi \\[5pt]
3\theta &=& \frac{17\pi}{6} \\[5pt]
\theta &=& \frac{17}{18}\pi \\[5pt]
\end{eqnarray}となります。
解答
オカキク:2518
ケコサシス:61718
解答編 つづき
問題
(2) $0 \leqq \theta \lt \pi$ のとき、方程式
\[ \cos\left(\theta + \frac{\pi}{6}\right) = \cos 2\theta \]の解は
\[ \theta = \frac{\pi}{\myBox{セ}} , \frac{\myBox{ソタ}}{\myBox{チツ}}\pi \]である。
解説
(2)
まず、角度が等しいとき、つまり、\[ \theta+\frac{\pi}{6}=2\theta \]のときがあります。これは $\sin$ のときと同じで、 $\theta=\dfrac{\pi}{6}$ です。
次に、角度が異なるときを考えます。 $\cos$ が等しいのは、 $x$ 座標が等しいときです。 $0\leqq \theta\leqq \dfrac{\pi}{2}$ のときは、 $0\leqq \beta\leqq \pi$ なので、 $\cos\alpha$ と $\cos\beta$ が等しくなることはありません(角度が異なって $\cos$ が一致することがないからです)。
$\dfrac{\pi}{2} \lt \theta\lt \pi$ のときは、 $0\leqq \beta\leqq 2\pi$ なので、次のような状況だと、 $x$ 座標が等しくなります。
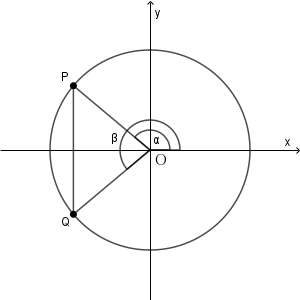
2つの角の平均が $\pi$ のとき、つまり、 $\alpha+\beta=2\pi$ のときです。これを解くと
\begin{eqnarray}
\theta+\frac{\pi}{6}+2\theta &=& 2\pi \\[5pt]
3\theta &=& \frac{11\pi}{6} \\[5pt]
\theta &=& \frac{11}{18}\pi \\[5pt]
\end{eqnarray}となります。
解答
セ:6
ソタチツ:1118