共通テスト 数学II・数学B 2025年度旧課程 第4問 解説
【必答問題】
問題編
問題
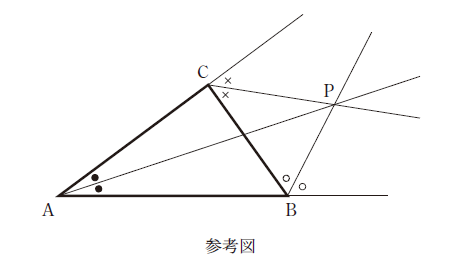
$\triangle \mathrm{ABC}$ において、内角 $\angle \mathrm{A}$ の二等分線と、頂点 $\mathrm{B}$、$\mathrm{C}$ それぞれにおける外角の二等分線の $3$ 直線は、$1$ 点で交わることが知られている。この点を $\mathrm{P}$ とする。
いま、$\mathrm{O}$ を原点とする座標平面において、$2$ 点 $\mathrm{A}$、$\mathrm{B}$ の座標はそれぞれ $(-1, 0)$、$(1, 0)$ であるとする。また、$S$ を中心が $\mathrm{O}$、半径が $1$ の円周の $y$ 座標が正の部分とし、点 $\mathrm{C}$ は $S$ 上を動くものとする。このとき、$\angle \mathrm{BAC} = \theta$ とすると、$0 \lt \theta \lt \dfrac{\pi}{2}$ であることに注意する。
(1) 太郎さんは、$\mathrm{C}$ が $S$ 上を動くときの $\mathrm{P}$ の軌跡を考えることにした。
(i) 直線 $\mathrm{AP}$ の傾きを $m$ とおくと、$m = \dBox{ア}$ であり、直線 $\mathrm{AP}$ の方程式は
\[ y = m(x + 1) \quad \cdots \text{①} \]となる。また、$\triangle \mathrm{ABC}$ の頂点 $\mathrm{B}$ における外角の大きさは $\theta + \dfrac{\pi}{2}$ であるから、直線 $\mathrm{BP}$ の傾きは $\dBox{イ}$ である。よって、等式
\[ \tan(\alpha + \beta) = \dfrac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta} \]により、直線 $\mathrm{BP}$ の方程式は $m$ を用いて
\[ y = \dBox{ウ} (x - 1) \quad \cdots \text{②} \]と表せる。太郎さんは $\mathrm{P}$ の座標を $(x, y)$ として、$\mathrm{P}$ が直線 $\mathrm{AP}$ 上と直線 $\mathrm{BP}$ 上にあるという条件から、$x, y$ の満たす方程式を求めることにした。
① から得られる $m = \dfrac{y}{x + 1}$ を ② に代入して整理すると、方程式
\[ x^2 + y^2 - \myBox{エ} y - \myBox{オ} = 0 \]が得られる。この方程式が表す図形は、中心が点 $(0, \myBox{カ})$ 、半径が $\sqrt{\myBox{キ}}$ の円である。この円を $E$ とする。$\dbox{ア},$ $\dbox{イ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\tan \theta$
1: $\dfrac{1}{2} \tan \theta$
2: $\tan \dfrac{\theta}{2}$
3: $\tan\left(\theta + \dfrac{\pi}{2}\right)$
4: $\dfrac{1}{2} \tan\left(\theta + \dfrac{\pi}{2}\right)$
5: $\tan\left(\dfrac{\theta}{2} + \dfrac{\pi}{4}\right)$$\dbox{ウ}$ の解答群
0: $m$
1: $m + 1$
2: $2m$3: $\dfrac{1}{m}$
4: $\dfrac{2m + 1}{2 - m}$
5: $\dfrac{m + 1}{1 - m}$
6: $\dfrac{1 - m}{1 + m}$
7: $\dfrac{2m}{1 - m^2}$
(ii) 太郎さんと花子さんは、(i) で得られた円 $E$ について話している。
- 円 $E$ が $\mathrm{P}$ の軌跡なのかな。
- $\mathrm{P}$ の $y$ 座標が $0$ 以下になることはないから、$\mathrm{P}$ の軌跡は円 $E$ 全体ではないね。
- そうだね。軌跡は円 $E$ のどの部分だろう。
- ためしに直線 $\mathrm{AP}$ 上の点が満たす条件を調べてみようか。
$0 \lt \theta \lt \dfrac{\pi}{2}$ に注意すると、直線 $\mathrm{AP}$ の傾き $m$ がとり得る値の範囲は $\dBox{ク}$ であることがわかる。よって、① から、直線 $\mathrm{AP}$ 上の $y \gt 0$ を満たす点 $(x, y)$ について、$x, y$ は $\dBox{ケ}$ を満たす。
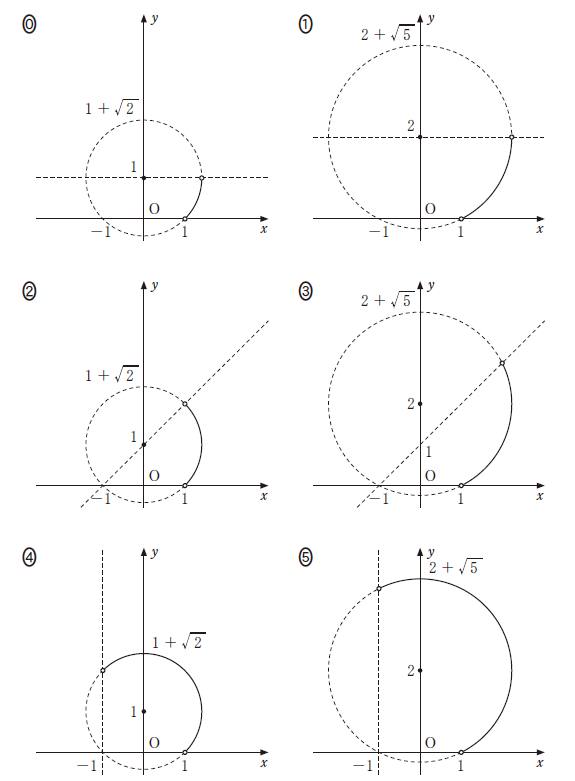
$E$ 上の点 $(x, y)$ のうち、$\dbox{ケ}$ を満たすものすべてを図示すると、$\dBox{コ}$ の実線部分である。
逆に、$\dbox{コ}$ の実線部分上にある点は、$S$ 上の適当な点 $\mathrm{C}$ を選ぶことにより、内角 $\angle \mathrm{A}$ の二等分線と頂点 $\mathrm{B}$ における外角の二等分線の交点になることがわかる。
したがって、$\mathrm{P}$ の軌跡は $\dbox{コ}$ の実線部分である。$\dbox{ク}$ の解答群
0: $m \gt 0$
1: $m \gt 1$
2: $0 \lt m \lt 1$
3: $0 \lt m \lt 2$$\dbox{ケ}$ の解答群
0: $0 \lt x + 1 \lt y$
1: $0 \lt y \lt x + 1$
2: $0 \lt 2(x - 1) \lt y$
3: $0 \lt y \lt 2(x - 1)$$\dbox{コ}$ については、最も適当なものを、次の 0 ~ 5 のうちから一つ選べ。
(2) $\triangle \mathrm{ABP}$ において、$\angle \mathrm{BAP}$ の二等分線と頂点 $\mathrm{B}$、$\mathrm{P}$ それぞれにおける外角の二等分線の $3$ 直線が交わる点を $\mathrm{Q}$ とする。$\mathrm{P}$ が (1) で求めた $\dbox{コ}$ の実線部分を動くとき、$\mathrm{Q}$ の軌跡を考える。
$\mathrm{Q}$ の座標を $(x, y)$ とおき、直線 $\mathrm{AQ}$ の傾きを $m'$ とする。直線 $\mathrm{BQ}$ の傾きは $m'$ を用いて $\dBox{サ}$ と表される。
$\mathrm{Q}$ の軌跡は、直線 $\mathrm{BQ}$ の方程式に $m' = \dBox{シ}$ を代入して得られる $x, y$ の方程式が表す図形の一部であることがわかる。$\dbox{サ}$ の解答群
0: $m' + 1$1: $m' + \tan \dfrac{\pi}{8}$
2: $\dfrac{1}{m'}$
3: $\dfrac{2m' + 1}{2 - m'}$
4: $\dfrac{m' + 1}{1 - m'}$
5: $\dfrac{1 - m'}{1 + m'}$
6: $\dfrac{m' + \tan \dfrac{\pi}{8}}{1 - m' \tan \dfrac{\pi}{8}}$
7: $\dfrac{\tan \dfrac{\pi}{8} - m'}{1 + m' \tan \dfrac{\pi}{8}}$
$\dbox{シ}$ の解答群
0: $\dfrac{y}{x - 1}$
1: $\dfrac{y}{x + 1}$
2: $\dfrac{y}{1 - x}$
3: $\dfrac{y}{x - \tan \dfrac{\pi}{8}}$
4: $\dfrac{y}{x + \tan \dfrac{\pi}{8}}$
5: $\dfrac{y}{\tan \dfrac{\pi}{8} - x}$
考え方
【必答問題】
解答編
問題
$\triangle \mathrm{ABC}$ において、内角 $\angle \mathrm{A}$ の二等分線と、頂点 $\mathrm{B}$、$\mathrm{C}$ それぞれにおける外角の二等分線の $3$ 直線は、$1$ 点で交わることが知られている。この点を $\mathrm{P}$ とする。
いま、$\mathrm{O}$ を原点とする座標平面において、$2$ 点 $\mathrm{A}$、$\mathrm{B}$ の座標はそれぞれ $(-1, 0)$、$(1, 0)$ であるとする。また、$S$ を中心が $\mathrm{O}$、半径が $1$ の円周の $y$ 座標が正の部分とし、点 $\mathrm{C}$ は $S$ 上を動くものとする。このとき、$\angle \mathrm{BAC} = \theta$ とすると、$0 \lt \theta \lt \dfrac{\pi}{2}$ であることに注意する。
(1) 太郎さんは、$\mathrm{C}$ が $S$ 上を動くときの $\mathrm{P}$ の軌跡を考えることにした。
(i) 直線 $\mathrm{AP}$ の傾きを $m$ とおくと、$m = \dBox{ア}$ であり、直線 $\mathrm{AP}$ の方程式は
\[ y = m(x + 1) \quad \cdots \text{①} \]となる。また、$\triangle \mathrm{ABC}$ の頂点 $\mathrm{B}$ における外角の大きさは $\theta + \dfrac{\pi}{2}$ であるから、直線 $\mathrm{BP}$ の傾きは $\dBox{イ}$ である。よって、等式
\[ \tan(\alpha + \beta) = \dfrac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta} \]により、直線 $\mathrm{BP}$ の方程式は $m$ を用いて
\[ y = \dBox{ウ} (x - 1) \quad \cdots \text{②} \]と表せる。太郎さんは $\mathrm{P}$ の座標を $(x, y)$ として、$\mathrm{P}$ が直線 $\mathrm{AP}$ 上と直線 $\mathrm{BP}$ 上にあるという条件から、$x, y$ の満たす方程式を求めることにした。
① から得られる $m = \dfrac{y}{x + 1}$ を ② に代入して整理すると、方程式
\[ x^2 + y^2 - \myBox{エ} y - \myBox{オ} = 0 \]が得られる。この方程式が表す図形は、中心が点 $(0, \myBox{カ})$ 、半径が $\sqrt{\myBox{キ}}$ の円である。この円を $E$ とする。$\dbox{ア},$ $\dbox{イ}$ の解答群(同じものを繰り返し選んでもよい。)
0: $\tan \theta$
1: $\dfrac{1}{2} \tan \theta$
2: $\tan \dfrac{\theta}{2}$
3: $\tan\left(\theta + \dfrac{\pi}{2}\right)$
4: $\dfrac{1}{2} \tan\left(\theta + \dfrac{\pi}{2}\right)$
5: $\tan\left(\dfrac{\theta}{2} + \dfrac{\pi}{4}\right)$$\dbox{ウ}$ の解答群
0: $m$
1: $m + 1$
2: $2m$3: $\dfrac{1}{m}$
4: $\dfrac{2m + 1}{2 - m}$
5: $\dfrac{m + 1}{1 - m}$
6: $\dfrac{1 - m}{1 + m}$
7: $\dfrac{2m}{1 - m^2}$
解説
(1)(i)
\[ \angle\mathrm{BAP}=\dfrac{1}{2}\angle\mathrm{BAC}=\dfrac{1}{2} \theta \]なので、直線 $\mathrm{AP}$ の傾き $m$ は\[ m=\tan\frac{\theta}{2} \]となります。
$\mathrm{C}$ は $\mathrm{AB}$ を直径とする円周上の点なので、 $\angle\mathrm{C}=\dfrac{\pi}{2}$ だから、点 $\mathrm{B}$ における外角の大きさは $\theta+\dfrac{\pi}{2}$ なので、直線 $\mathrm{BP}$ の傾きは\[ \tan\left(\frac{\theta}{2}+\dfrac{\pi}{4}\right) \]となります。 $\tan$ の加法定理から
\begin{eqnarray}
\tan\left(\frac{\theta}{2}+\dfrac{\pi}{4}\right)
&=&
\frac{\tan\frac{\theta}{2}+\tan\frac{\pi}{4}}{1-\tan\frac{\theta}{2}\tan\frac{\pi}{4}} \\[5pt]
&=&
\frac{m+1}{1-m\cdot 1} \\[5pt]
\end{eqnarray}となるので、直線 $\mathrm{BP}$ の方程式は\[ y=\frac{m+1}{1-m}(x-1) \]だとわかります。
直線 $\mathrm{AP}$ の方程式を変形すると $m=\dfrac{y}{x+1}$ となるので、これを直線 $\mathrm{BP}$ の方程式に代入して
\begin{eqnarray}
y &=& \frac{m+1}{1-m}(x-1) \\[5pt]
y &=& \frac{\frac{y}{x+1}+1}{1-\frac{y}{x+1}}(x-1) \\[5pt]
y &=& \frac{y+(x+1)}{(x+1)-y}(x-1) \\[5pt]
(x+1-y)y &=& (y+x+1)(x-1) \\[5pt]
xy+y-y^2 &=& xy+x^2+x-y-x-1 \\[5pt]
y-y^2 &=& x^2-y-1 \\[5pt]
\end{eqnarray}となります。左辺と右辺を入れ替えてさらに整理すると
\begin{eqnarray}
x^2+y^2-2y-1 &=& 0 \\[5pt]
x^2+(y-1)^2 &=& 2 \\[5pt]
\end{eqnarray}となるので、中心が $(0,1)$ で半径が $\sqrt{2}$ の円だとわかります。
解答
ア:2
イウ:55
エオカキ:2112
解答編 つづき
問題
(ii) 太郎さんと花子さんは、(i) で得られた円 $E$ について話している。
- 円 $E$ が $\mathrm{P}$ の軌跡なのかな。
- $\mathrm{P}$ の $y$ 座標が $0$ 以下になることはないから、$\mathrm{P}$ の軌跡は円 $E$ 全体ではないね。
- そうだね。軌跡は円 $E$ のどの部分だろう。
- ためしに直線 $\mathrm{AP}$ 上の点が満たす条件を調べてみようか。
$0 \lt \theta \lt \dfrac{\pi}{2}$ に注意すると、直線 $\mathrm{AP}$ の傾き $m$ がとり得る値の範囲は $\dBox{ク}$ であることがわかる。よって、① から、直線 $\mathrm{AP}$ 上の $y \gt 0$ を満たす点 $(x, y)$ について、$x, y$ は $\dBox{ケ}$ を満たす。
$E$ 上の点 $(x, y)$ のうち、$\dbox{ケ}$ を満たすものすべてを図示すると、$\dBox{コ}$ の実線部分である。
逆に、$\dbox{コ}$ の実線部分上にある点は、$S$ 上の適当な点 $\mathrm{C}$ を選ぶことにより、内角 $\angle \mathrm{A}$ の二等分線と頂点 $\mathrm{B}$ における外角の二等分線の交点になることがわかる。
したがって、$\mathrm{P}$ の軌跡は $\dbox{コ}$ の実線部分である。$\dbox{ク}$ の解答群
0: $m \gt 0$
1: $m \gt 1$
2: $0 \lt m \lt 1$
3: $0 \lt m \lt 2$$\dbox{ケ}$ の解答群
0: $0 \lt x + 1 \lt y$
1: $0 \lt y \lt x + 1$
2: $0 \lt 2(x - 1) \lt y$
3: $0 \lt y \lt 2(x - 1)$$\dbox{コ}$ については、最も適当なものを、次の 0 ~ 5 のうちから一つ選べ。
解説
(1)(ii)
$0\lt \theta\lt\dfrac{\pi}{2}$ であり、 $m=\tan\dfrac{\theta}{2}$ なので、 $m$ のとり得る値の範囲は\[ 0\lt m\lt 1 \]です。
$y=m(x+1)$ で $y\gt 0$ のときに $x+1\gt 0$ なので、 $0\lt m\lt 1$ は、
\begin{eqnarray}
0 \lt \frac{y}{x+1} \lt 1 \\[5pt]
0 \lt y \lt x+1 \\[5pt]
\end{eqnarray}と同値です。
次に、図示したものを選びます。 $E$ は中心が $(0,1)$ で半径が $\sqrt{2}$ の円なので、0,2,4 のどれかです。
さらに、 $0\lt y\lt x+1$ を満たしているものは、 2 だとわかります。
解答
クケ:21
コ:2
解答編 つづき
問題
(2) $\triangle \mathrm{ABP}$ において、$\angle \mathrm{BAP}$ の二等分線と頂点 $\mathrm{B}$、$\mathrm{P}$ それぞれにおける外角の二等分線の $3$ 直線が交わる点を $\mathrm{Q}$ とする。$\mathrm{P}$ が (1) で求めた $\dbox{コ}$ の実線部分を動くとき、$\mathrm{Q}$ の軌跡を考える。
$\mathrm{Q}$ の座標を $(x, y)$ とおき、直線 $\mathrm{AQ}$ の傾きを $m'$ とする。直線 $\mathrm{BQ}$ の傾きは $m'$ を用いて $\dBox{サ}$ と表される。
$\mathrm{Q}$ の軌跡は、直線 $\mathrm{BQ}$ の方程式に $m' = \dBox{シ}$ を代入して得られる $x, y$ の方程式が表す図形の一部であることがわかる。$\dbox{サ}$ の解答群
0: $m' + 1$1: $m' + \tan \dfrac{\pi}{8}$
2: $\dfrac{1}{m'}$
3: $\dfrac{2m' + 1}{2 - m'}$
4: $\dfrac{m' + 1}{1 - m'}$
5: $\dfrac{1 - m'}{1 + m'}$
6: $\dfrac{m' + \tan \dfrac{\pi}{8}}{1 - m' \tan \dfrac{\pi}{8}}$
7: $\dfrac{\tan \dfrac{\pi}{8} - m'}{1 + m' \tan \dfrac{\pi}{8}}$
$\dbox{シ}$ の解答群
0: $\dfrac{y}{x - 1}$
1: $\dfrac{y}{x + 1}$
2: $\dfrac{y}{1 - x}$
3: $\dfrac{y}{x - \tan \dfrac{\pi}{8}}$
4: $\dfrac{y}{x + \tan \dfrac{\pi}{8}}$
5: $\dfrac{y}{\tan \dfrac{\pi}{8} - x}$
解説
(2)
(1)と同様に考えます。
$\angle\mathrm{BAQ}=\dfrac{1}{2}\angle\mathrm{BAP}=\dfrac{1}{4}\theta$ なので、 $\mathrm{AQ}$ の傾き $m'$ は $\tan\dfrac{\theta}{4}$ です。
コのグラフを見ると、$\angle\mathrm{APB}$ は 中心角が $90^{\circ}$ だとわかるので、 $\angle\mathrm{APB}=\dfrac{1}{4}\pi$ です。なので、 $\triangle\mathrm{PAB}$ の点 $\mathrm{B}$ における外角は\[ \frac{\theta}{2}+\frac{\pi}{4} \]だから、 $\mathrm{BQ}$ の傾きは\[ \tan\left(\dfrac{\theta}{4}+\dfrac{\pi}{8}\right) \]と書けます。加法定理を使って
\begin{eqnarray}
& &
\tan\left(\dfrac{\theta}{4}+\dfrac{\pi}{8}\right) \\[5pt]
&=&
\frac{\tan\dfrac{\theta}{4}+\tan\dfrac{\pi}{8}}{1-\tan\dfrac{\theta}{4}\tan\dfrac{\pi}{8}} \\[5pt]
&=&
\frac{m'+\tan\dfrac{\pi}{8}}{1-m'\tan\dfrac{\pi}{8}} \\[5pt]
\end{eqnarray}となることがわかります。
$\mathrm{Q}$ の軌跡は、先ほどと同じようにすれば直線 $\mathrm{AQ}$ の方程式を変形したものを代入すれば求められます。直線 $\mathrm{AQ}$ の方程式は\[ y=m'(x+1) \]なので、 $m'=\dfrac{y}{x+1}$ を代入すればいいです。
解答
サシ:61