共通テスト数学I・数学A 2025年度試作問題第2問 [2] 解説

🕒 2025/01/17

2025年度より実施される、新学習指導要領に対応した大学入試共通テストの試作問題（2022年11月発表）です。詳細はこちら。

【必答問題】

問題編

問題

　太郎さんと花子さんは、社会のグローバル化に伴う都市間の国際競争において、都市周辺にある国際空港の利便性が重視されていることを知った。そこで、日本を含む世界の主な 40 の国際空港それぞれから最も近い主要ターミナル駅へ鉄道等で移動するときの「移動距離」、「所要時間」、「費用」を調べた。なお、「所要時間」と「費用」は各国とも午前 10 時台で調査し、「費用」は調査時点の為替レートで日本円に換算した。

以下では、データが与えられた際、次の値を外れ値とする。

　「(第１四分位数)－1.5×(四分位範囲)」以下のすべての値
　「(第３四分位数)＋1.5×(四分位範囲)」以上のすべての値

(1) 次のデータは、40 の国際空港からの「移動距離」（単位はkm）を並べたものである。

　56 48 47 42 40 38 38 36 28 25
　25 24 23 22 22 21 21 20 20 20
　20 20 19 18 16 16 15 15 14 13
　13 12 11 11 10 10 10 8 7 6

このデータにおいて、四分位範囲は $\myBox{タチ}$ であり、外れ値の個数は $\myBox{ツ}$ である。

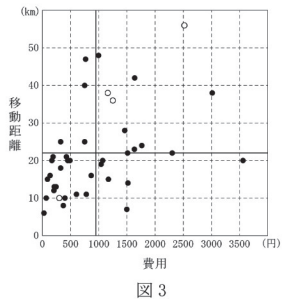
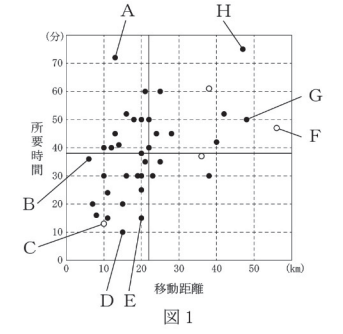
(2) 図 1 は「移動距離」と「所要時間」の散布図、図 2 は「所要時間」と「費用」の散布図、図 3 は「費用」と「移動距離」の散布図である。ただし、白丸は日本の空港、黒丸は日本以外の空港を表している。また、「移動距離」、「所要時間」、「費用」の平均値はそれぞれ 22、38、950 であり、散布図に実線で示している。

(i) 40 の国際空港について、「所要時間」を「移動距離」で割った「1 kmあたりの所要時間」を考えよう。外れ値を＊で示した「1 kmあたりの所要時間」の箱ひげ図は $\dBox{テ}$ であり、外れ値は図 1 のＡ～Ｈのうちの $\dBox{ト}$ と $\dBox{ナ}$ である。

$\dbox{テ}$ については、最も適当なものを、次の 0 ～ 4 のうちから一つ選べ。

$\dbox{ト},\ \dbox{ナ}$ の解答群（解答の順序は問わない。）

　0: Ａ
　1: Ｂ
　2: Ｃ
　3: Ｄ
　4: Ｅ
　5: Ｆ
　6: Ｇ
　7: Ｈ

(ii) ある国で、次のような新空港が建設される計画があるとする。

移動距離 (km) 所要時間 (分) 費用 (円)

22 38 950

　次の (I)、(II)、(III) は、40 の国際空港にこの新空港を加えたデータに関する記述である。

　(I) 新空港は、日本の四つのいずれの空港よりも、「費用」は高いが「所要時間」は短い。

　(II) 「移動距離」の標準偏差は、新空港を加える前後で変化しない。

　(III) 図 1、図 2、図 3 のそれぞれの二つの変量について、変量間の相関係数は、新空港を加える前後で変化しない。

(I)、(II)、(III) の正誤の組合せとして正しいものは $\dBox{ニ}$ である。

　$\dbox{ニ}$ の解答群

　0: (I) 正　(II) 正　(III) 正
　1: (I) 正　(II) 正　(III) 誤
　2: (I) 正　(II) 誤　(III) 正
　3: (I) 正　(II) 誤　(III) 誤

　4: (I) 誤　(II) 正　(III) 正
　5: (I) 誤　(II) 正　(III) 誤
　6: (I) 誤　(II) 誤　(III) 正
　7: (I) 誤　(II) 誤　(III) 誤

(3) 太郎さんは、調べた空港のうちの一つであるＰ空港で、利便性に関するアンケート調査が実施されていることを知った。

Ｐ空港を利用した 30 人に、Ｐ空港は便利だと思うかどうかをたずねたとき、どのくらいの人が「便利だと思う」と回答したら、Ｐ空港の利用者全体のうち便利だと思う人の方が多いとしてよいのかな。

例えば、20 人だったらどうかな。

　二人は、30 人のうち 20 人が「便利だと思う」と回答した場合に、「Ｐ空港は便利だと思う人の方が多い」といえるかどうかを、次の方針で考えることにした。

方針

"Ｐ空港の利用者全体のうちで「便利だと思う」と回答する割合と、「便利だと思う」と回答しない割合が等しい" という仮説をたてる。

この仮説のもとで、30 人抽出したうちの 20 人以上が「便利だと思う」と回答する確率が 5％未満であれば、その仮説は誤っていると判断し、5％以上であれば、その仮説は誤っているとは判断しない。

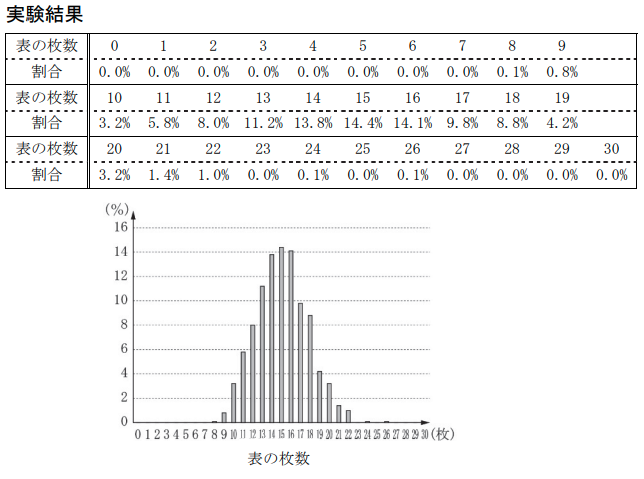
次の実験結果は、30 枚の硬貨を投げる実験を 1000 回行ったとき、表が出た枚数ごとの回数の割合を示したものである。

　実験結果を用いると、30 枚の硬貨のうち 20 枚以上が表となった割合は $\myBox{ヌ}\ .\ \myBox{ネ}$ ％である。これを、30 人のうち 20 人以上が「便利だと思う」と回答する確率とみなし、方針に従うと、「便利だと思う」と回答する割合と、「便利だと思う」と回答しない割合が等しいという仮説は $\dBox{ノ}$ 、Ｐ空港は便利だと思う人の方が $\dBox{ハ}$ 。

$\dbox{ノ}$ 、 $\dbox{ハ}$ については、最も適当なものを、次のそれぞれの解答群から一つずつ選べ。

$\dbox{ノ}$ の解答群
　0: 誤っていると判断され
　1: 誤っているとは判断されず

$\dbox{ハ}$ の解答群
　0: 多いといえる
　1: 多いとはいえない

移動距離 (km)	所要時間 (分)	費用 (円)
22	38	950

考え方

新課程の範囲は、序盤の外れ値と後半の仮説検定の部分です。

外れ値は単体ではなくて、四分位範囲もわかっていないと計算ができません。

仮説検定は、どのような考え方かがわかっていれば、それほど難しくはないでしょう。

他にも、1kmあたりの所要時間を散布図からどう読むか、新しいデータを追加して、標準偏差や相関係数がどう変わるかなど、他の年でも聞かれそうな内容が含まれています。

【必答問題】

解答編

問題

　太郎さんと花子さんは、社会のグローバル化に伴う都市間の国際競争において、都市周辺にある国際空港の利便性が重視されていることを知った。そこで、日本を含む世界の主な 40 の国際空港それぞれから最も近い主要ターミナル駅へ鉄道等で移動するときの「移動距離」、「所要時間」、「費用」を調べた。なお、「所要時間」と「費用」は各国とも午前 10 時台で調査し、「費用」は調査時点の為替レートで日本円に換算した。

以下では、データが与えられた際、次の値を外れ値とする。

　「(第１四分位数)－1.5×(四分位範囲)」以下のすべての値
　「(第３四分位数)＋1.5×(四分位範囲)」以上のすべての値

(1) 次のデータは、40 の国際空港からの「移動距離」（単位はkm）を並べたものである。

　56 48 47 42 40 38 38 36 28 25
　25 24 23 22 22 21 21 20 20 20
　20 20 19 18 16 16 15 15 14 13
　13 12 11 11 10 10 10 8 7 6

このデータにおいて、四分位範囲は $\myBox{タチ}$ であり、外れ値の個数は $\myBox{ツ}$ である。

解説

値の個数は40なので、まず20個ずつに分けられます。第1四分位数は小さい方のデータの中央値なので、小さい方から10番目と11番目の平均です。どちらも13なので、第1四分位数は、13です。

第3四分位数は大きい方から10番目と11番目の平均です。どちらも25なので、第3四分位数は25です。

なので、四分位範囲は $25-13=12$ と求められます。

問題文にある通り、外れ値は

　$13-1.5\times 12$ 以下
　$25+1.5\times 12$ 以上

の値なので、

　$-5$ 以下
　$43$ 以上

だから、56, 48, 47 の3つだとわかります。

解答

タチ：12
ツ：3

解答編　つづき

問題

(2) 図 1 は「移動距離」と「所要時間」の散布図、図 2 は「所要時間」と「費用」の散布図、図 3 は「費用」と「移動距離」の散布図である。ただし、白丸は日本の空港、黒丸は日本以外の空港を表している。また、「移動距離」、「所要時間」、「費用」の平均値はそれぞれ 22、38、950 であり、散布図に実線で示している。

(i) 40 の国際空港について、「所要時間」を「移動距離」で割った「1 kmあたりの所要時間」を考えよう。外れ値を＊で示した「1 kmあたりの所要時間」の箱ひげ図は $\dBox{テ}$ であり、外れ値は図 1 のＡ～Ｈのうちの $\dBox{ト}$ と $\dBox{ナ}$ である。

$\dbox{テ}$ については、最も適当なものを、次の 0 ～ 4 のうちから一つ選べ。

$\dbox{ト},\ \dbox{ナ}$ の解答群（解答の順序は問わない。）

　0: Ａ
　1: Ｂ
　2: Ｃ
　3: Ｄ
　4: Ｅ
　5: Ｆ
　6: Ｇ
　7: Ｈ

解説

「1 kmあたりの所要時間」は、「所要時間」を「移動距離」で割ったものなので、図1 を使います。縦の値を横の値で割っているので、点と原点を結んだ直線の傾きに対応することがわかります。

例えば、選択肢 0 や 4 を見ると、中央値は $4$ を超えていることがわかります。

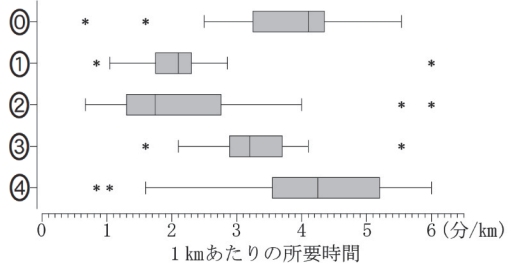
これは、傾きが $4$ を超えているということです。ためしに、図1 で傾きが $4$ の直線（原点と(10,40)を通る直線）をひいてみると、それより上にある点はほとんどありません。中央値なら、ざっくりいうと、上にも下にも半分くらいの点がないとダメなので、中央値が $4$ を超えることはないとわかります。

同じ理由で、傾きが $3$ より大きいということもないので、選択肢 3 も違います。

選択肢 1 と 2 では、中央値で判断するのは難しそうなので、大きな値を見て考えてみます。選択肢 1 の場合、外れ値 $6$ の次は $3$ あたりの値をとっています。しかし、傾きが $4$ の直線（原点と(10,40)を通る直線）上に1つ点があるので、選択肢 1 にはこれに対応する値がないことがわかります。

このことから、選択肢 2 が正しいことがわかります。

選択肢 2 の箱ひげ図から、大きな値2つが外れ値だとわかります。

図1 で見ると、傾きが大きいものは、ＡとＢであり、どちらも6くらいなので、箱ひげ図の内容とも会っていることがわかります。

解答

テ：2
ト・ナ：0・1

解答編　つづき

問題

(ii) ある国で、次のような新空港が建設される計画があるとする。

移動距離 (km) 所要時間 (分) 費用 (円)

22 38 950

　次の (I)、(II)、(III) は、40 の国際空港にこの新空港を加えたデータに関する記述である。

　(I) 新空港は、日本の四つのいずれの空港よりも、「費用」は高いが「所要時間」は短い。

　(II) 「移動距離」の標準偏差は、新空港を加える前後で変化しない。

　(III) 図 1、図 2、図 3 のそれぞれの二つの変量について、変量間の相関係数は、新空港を加える前後で変化しない。

(I)、(II)、(III) の正誤の組合せとして正しいものは $\dBox{ニ}$ である。

　$\dbox{ニ}$ の解答群

　0: (I) 正　(II) 正　(III) 正
　1: (I) 正　(II) 正　(III) 誤
　2: (I) 正　(II) 誤　(III) 正
　3: (I) 正　(II) 誤　(III) 誤

　4: (I) 誤　(II) 正　(III) 正
　5: (I) 誤　(II) 正　(III) 誤
　6: (I) 誤　(II) 誤　(III) 正
　7: (I) 誤　(II) 誤　(III) 誤

移動距離 (km)	所要時間 (分)	費用 (円)
22	38	950

解説

22, 38, 950 という値は、もとのデータの平均値と一致しています。そのため、グラフ内の実線がそのまま利用できます。

(I) について考えます。「新空港の費用は日本の費用より高い」とありますが、実線と白丸を比べると、左下に実線より下に白丸があります。

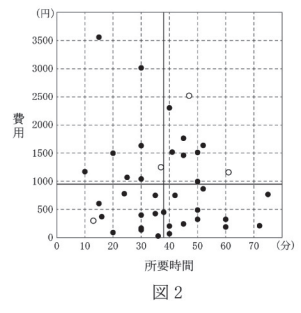
所要時間も実線より左に白丸があるので、いずれにしても、誤りだとわかります。

(II) は、標準偏差の求め方を考えればわかります。標準偏差は、各データと平均値の差を2乗し、足し合わせて、データ数で割ってルートをとったものです。

平均値と同じ値を追加するので、平均値は変わらず、「各データと平均値の差」なども変わらないですが、「データ数で割る」ところが変わります。分子は変わらないけど分母が変わるので、値は変わります。なので、誤りです。

(III) も求め方から考えることもできますが、意味から考えてもわかります。相関係数は、「片方が大きいほどもう片方も大きい」という度合いを表しています。基準は平均値なので、基準となる値を追加してもこの度合いは変化しません。なので、相関係数は変わりません。

求め方でいうと、共分散をそれぞれの標準偏差で割ることになりますが、共分散は $\frac{40}{41}$ 倍、標準偏差はそれぞれ $\sqrt{\frac{40}{41}}$ 倍となり、全体では変化しないことになります。

以上から、誤、誤、正となります。

解答

ニ：6

解答編　つづき

問題

(3) 太郎さんは、調べた空港のうちの一つであるＰ空港で、利便性に関するアンケート調査が実施されていることを知った。

Ｐ空港を利用した 30 人に、Ｐ空港は便利だと思うかどうかをたずねたとき、どのくらいの人が「便利だと思う」と回答したら、Ｐ空港の利用者全体のうち便利だと思う人の方が多いとしてよいのかな。

例えば、20 人だったらどうかな。

　二人は、30 人のうち 20 人が「便利だと思う」と回答した場合に、「Ｐ空港は便利だと思う人の方が多い」といえるかどうかを、次の方針で考えることにした。

方針

"Ｐ空港の利用者全体のうちで「便利だと思う」と回答する割合と、「便利だと思う」と回答しない割合が等しい" という仮説をたてる。

この仮説のもとで、30 人抽出したうちの 20 人以上が「便利だと思う」と回答する確率が 5％未満であれば、その仮説は誤っていると判断し、5％以上であれば、その仮説は誤っているとは判断しない。

次の実験結果は、30 枚の硬貨を投げる実験を 1000 回行ったとき、表が出た枚数ごとの回数の割合を示したものである。

　実験結果を用いると、30 枚の硬貨のうち 20 枚以上が表となった割合は $\myBox{ヌ}\ .\ \myBox{ネ}$ ％である。これを、30 人のうち 20 人以上が「便利だと思う」と回答する確率とみなし、方針に従うと、「便利だと思う」と回答する割合と、「便利だと思う」と回答しない割合が等しいという仮説は $\dBox{ノ}$ 、Ｐ空港は便利だと思う人の方が $\dBox{ハ}$ 。

$\dbox{ノ}$ 、 $\dbox{ハ}$ については、最も適当なものを、次のそれぞれの解答群から一つずつ選べ。

$\dbox{ノ}$ の解答群
　0: 誤っていると判断され
　1: 誤っているとは判断されず

$\dbox{ハ}$ の解答群
　0: 多いといえる
　1: 多いとはいえない

解説

これは、仮説検定の問題です。

実験結果を見て、表が20以上の割合を足していきます。 $0.0$ を除外すると
\begin{eqnarray} 3.2+1.4+1.0+0.1+0.1=5.8 \end{eqnarray}だから、 $5.8$ ％と求められます。

方針によると、$5$ ％以上なので、仮説は誤っているとは判断しないため、Ｐ空港が便利だと思う人の方が多いとは言えないことがわかります。

この問題で何をやっているかをまとめてみましょう。

まず、30人にアンケートをとったら、20人が便利と答えた、という事実があります。これを「便利と思う人が多いからこの結果になった」のか「便利と思う人も思わない人も同じくらいいたけど、たまたまこの結果になった」のかを考えようとしたわけです。

そこで、もし同じくらいいたなら、コインを30回投げて20回以上表が出るくらいのことが起こったと考え、それってどれくらいの確率なんだろう、というのを計算したわけですね。唐突にコイン投げの実験が出てきましたが、これは「便利と思う人も思わない人も同じくらいいる」状況を表しています。

で、この確率がすごく小さければ、「同じくらいいたって考えるのは不自然で、便利だと思う人の方が多いと考えたほうが自然だよね」となるのですが、今回の計算では、別に確率が小さいわけではなかったので、「同じ割合じゃない、っていうこともできないし、便利だと思う人の方が多いともいえないね」という結論になった、という話です。