共通テスト 数学I・数学A 2025年度旧課程 第2問 [2] 解説

【必答問題】

問題編

問題

　太郎さんと花子さんは、社会生活基本調査の集計結果に、「睡眠」、「食事」、「通勤・通学」、「移動（通勤・通学を除く）」などの20種類の行動それぞれについての総平均時間と行動者平均時間が、47都道府県別に集計されていることを知った。

用語の説明

• 総平均時間……ある行動に費やした時間の調査対象者全員についての平均値（分）
• 行動者平均時間……ある行動に費やした時間の調査対象者全員から、その行動に費やした時間が0分の人を除いた調査対象者についての平均値（分）

　例えば、「通勤・通学」に費やした時間（分）が\[ 75, \ 0, \ 90, \ 60, \ 0 \]であったとき、これらの平均値 $\dfrac{75+0+90+60+0}{5} = 45$ が総平均時間であり、値が0である二つを除いた $75, \ 90, \ 60$ の平均値 $\dfrac{75+90+60}{3} = 75$ が行動者平均時間である。
　ここでは、平日における15歳以上を対象とした集計結果を用いて、都道府県ごとに値を算出している。
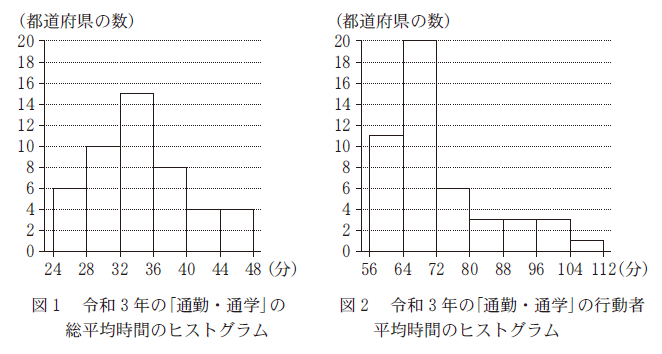
　なお、以下の図や表については、総務省のWebページをもとに作成している。

(1) 太郎さんと花子さんは、「通勤・通学」に費やした時間について調べることにした。図1と図2はそれぞれ、令和3年の「通勤・通学」の総平均時間と行動者平均時間のデータをヒストグラムに表したものである。以下、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。

(i) 図1から、令和3年の「通勤・通学」の総平均時間の最頻値は $\myBox{タチ}$ であり、同様に図2から、行動者平均時間の最頻値は $\myBox{ツテ}$ である。

(ii) 図1のヒストグラムに関して、各階級に含まれるデータの値がすべてその階級値に等しいと仮定する。このとき、令和3年の「通勤・通学」の総平均時間の平均値を $m$ とすると
\[ \myBox{トナ} \leqq m \lt \myBox{トナ} + 1 \]
である。

(iii) 次に、太郎さんと花子さんは、平成28年と令和3年の「通勤・通学」に費やした時間を比較することにした。
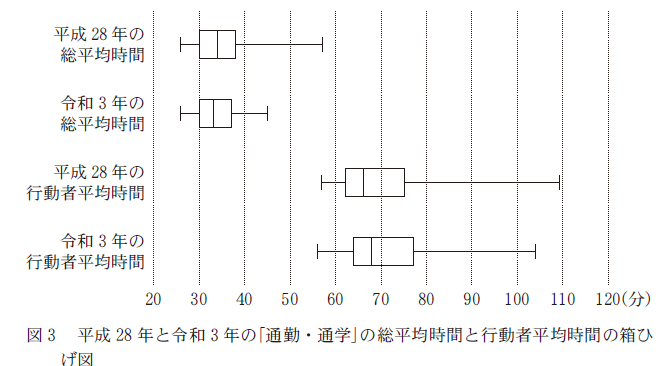
　図3は、平成28年の総平均時間、令和3年の総平均時間、平成28年の行動者平均時間、令和3年の行動者平均時間の箱ひげ図を並べたものである。
　ここで、あるデータにおける最大値から第3四分位数を引いた値を $H$ とする。そして平成28年の総平均時間、令和3年の総平均時間、平成28年の行動者平均時間、令和3年の行動者平均時間における $H$ を、それぞれ $H_1, \ H_2, \ H_3, \ H_4$ とする。

　次の(a)、(b)、(c)は、図3に関する記述である。

• (a) 令和3年の総平均時間の最大値は、令和3年の行動者平均時間の最小値より小さい。
• (b) 平成28年の総平均時間の四分位範囲は、平成28年の行動者平均時間の四分位範囲より小さい。
• (c) 総平均時間と行動者平均時間それぞれの、平成28年と令和3年の $H$ の変化を比較すると、 $\dfrac{H_2}{H_1} \gt \dfrac{H_4}{H_3}$ となる。

　(a)、(b)、(c)の正誤の組合せとして正しいものは $\dBox{ニ}$ である。

$\dbox{ニ}$ の解答群

0: (a) 正　(b) 正　(c) 正
1: (a) 正　(b) 正　(c) 誤
2: (a) 正　(b) 誤　(c) 正
3: (a) 正　(b) 誤　(c) 誤
4: (a) 誤　(b) 正　(c) 正
5: (a) 誤　(b) 正　(c) 誤
6: (a) 誤　(b) 誤　(c) 正
7: (a) 誤　(b) 誤　(c) 誤

(2) 太郎さんと花子さんは、令和3年における「通勤・通学」と「移動（通勤・通学を除く）」（以下、「移動」）に関し、それぞれの行動に費やした総平均時間と行動者平均時間の関係について話をしている。

• 通勤の途中で、ふだんの経路を大きくはずれて買い物に行ったり病院に行ったりする人もいるけど、こうした行動は「通勤・通学」ではなく、「移動」になるね。「通勤・通学」に費やした時間が長いほど、「移動」に費やした時間は長いのかな。
• じゃあ、それぞれに費やした時間の関係を調べてみようよ。

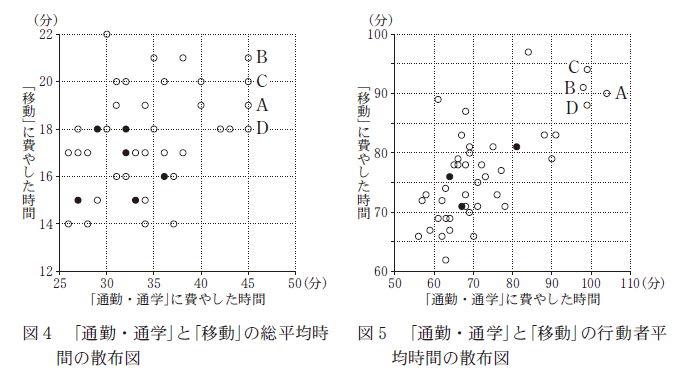
　図4と図5は「通勤・通学」と「移動」の総平均時間と行動者平均時間の散布図であり、図中の黒丸は、二つの点が完全に重なっていることを表している。なお、三つ以上の点が完全に重なっていることはない。ただし、図4と図5において、同じアルファベットを付している点は、同じ都道府県であることを表している。

(i) 図5から、「通勤・通学」の行動者平均時間が $60$ 以下で、かつ「移動」の行動者平均時間が $75$ 以下である都道府県の数は $\myBox{ヌ}$ である。

(ii) 図4における四つの点 $\mathrm{A, \ B, \ C, \ D}$ が表す都道府県では、「通勤・通学」の総平均時間が同じ値であるが、図5では「通勤・通学」の行動者平均時間について、点 $\mathrm{A}$ が表す都道府県の値は他の三つのどの都道府県の値よりも大きくなっていることがわかる。このようになるのは、 $\dBox{ネ}$ からである。

$\dbox{ネ}$ については、最も適当なものを、次の 0 ～ 3 のうちから一つ選べ。

0: 点 $\mathrm{A}$ が表す都道府県の「通勤・通学」に費やした時間が $0$ である人数の割合が、他の三つのどの都道府県の割合よりも大きい

1: 点 $\mathrm{A}$ が表す都道府県の「通勤・通学」に費やした時間が $0$ である人数の割合が、他の三つのどの都道府県の割合よりも小さい

2: 点 $\mathrm{A}$ が表す都道府県の「移動」に費やした時間が $0$ である人数の割合が、他の三つのどの都道府県の割合よりも大きい

3: 点 $\mathrm{A}$ が表す都道府県の「移動」に費やした時間が $0$ である人数の割合が、他の三つのどの都道府県の割合よりも小さい

(iii) 太郎さんと花子さんは、総平均時間と行動者平均時間のそれぞれの相関関係について調べることにした。
　「通勤・通学」と「移動」の総平均時間の相関係数は $0.36$ であった。「通勤・通学」と「移動」の行動者平均時間の相関係数を計算するために、表1のように平均値、標準偏差および共分散を求めた。

表1　「通勤・通学」と「移動」の行動者平均時間の平均値、標準偏差、共分散

	平均値	標準偏差	共分散
「通勤・通学」の行動者平均時間	$71.8$	$11.8$	$64.4$
「移動」の行動者平均時間	$76.6$	$7.9$

　表1を用いると、「通勤・通学」と「移動」の行動者平均時間の相関係数は $\myBox{ノ}$ である。

$\mybox{ノ}$ については、最も適当なものを、次の 0 ～ 7 のうちから一つ選べ。

0: $0.01$
1: $0.21$
2: $0.43$
3: $0.58$
4: $0.69$
5: $0.78$
6: $1.02$
7: $1.45$

考え方

行動者平均時間がはじめて見る概念ですが、結局は0を無視するだけということです。

(1)(ii)は、そのまま計算するのではなく工夫して計算しましょう。

(1)(iii)(c)は分かりにくい式ですが、ざっくりどれくらいの値になるかを考えて判断しましょう。

(2)の黒い点はあまり問題には関係ないです。点の数が47より少ないので、その理由を説明しているだけです。深く考えなくても構いません。

【必答問題】

解答編

問題

　太郎さんと花子さんは、社会生活基本調査の集計結果に、「睡眠」、「食事」、「通勤・通学」、「移動（通勤・通学を除く）」などの20種類の行動それぞれについての総平均時間と行動者平均時間が、47都道府県別に集計されていることを知った。

用語の説明

• 総平均時間……ある行動に費やした時間の調査対象者全員についての平均値（分）
• 行動者平均時間……ある行動に費やした時間の調査対象者全員から、その行動に費やした時間が0分の人を除いた調査対象者についての平均値（分）

　例えば、「通勤・通学」に費やした時間（分）が\[ 75, \ 0, \ 90, \ 60, \ 0 \]であったとき、これらの平均値 $\dfrac{75+0+90+60+0}{5} = 45$ が総平均時間であり、値が0である二つを除いた $75, \ 90, \ 60$ の平均値 $\dfrac{75+90+60}{3} = 75$ が行動者平均時間である。
　ここでは、平日における15歳以上を対象とした集計結果を用いて、都道府県ごとに値を算出している。
　なお、以下の図や表については、総務省のWebページをもとに作成している。

(1) 太郎さんと花子さんは、「通勤・通学」に費やした時間について調べることにした。図1と図2はそれぞれ、令和3年の「通勤・通学」の総平均時間と行動者平均時間のデータをヒストグラムに表したものである。以下、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。

(i) 図1から、令和3年の「通勤・通学」の総平均時間の最頻値は $\myBox{タチ}$ であり、同様に図2から、行動者平均時間の最頻値は $\myBox{ツテ}$ である。

解説

(1)(i)

図1 で一番多いのは、32以上36未満なので、最頻値は 34 です。

図2 で一番多いのは、64以上72未満なので、最頻値は 68 です。

解答

タチツテ：3468

解答編　つづき

問題

(ii) 図1のヒストグラムに関して、各階級に含まれるデータの値がすべてその階級値に等しいと仮定する。このとき、令和3年の「通勤・通学」の総平均時間の平均値を $m$ とすると
\[ \myBox{トナ} \leqq m \lt \myBox{トナ} + 1 \]
である。

解説

(1)(ii)

問題文より、 $26$ のデータが6個、などと考える、ということです。平均値は、次のように計算できます。
\begin{eqnarray} & & \frac{26\cdot 6 +30\cdot 10 +34\cdot 15 +38\cdot 8 +42\cdot 4 +46\cdot 4}{47} \\[5pt] &=& 26+\frac{0\cdot 6 +4\cdot 10 +8\cdot 15 +12\cdot 8 +16\cdot 4 +20\cdot 4}{47} \\[5pt] &=& 26+4\cdot \frac{0\cdot 6 +1\cdot 10 +2\cdot 15 +3\cdot 8 +4\cdot 4 +5\cdot 4}{47} \\[5pt] &=& 26+4\cdot \frac{0 +10 +30 +24 +16 +20}{47} \\[5pt] &=& 26+4\cdot \frac{100}{47} \\[5pt] &=& 26+8.\cdots \\[5pt] \end{eqnarray}こうして、平均値 $m$ は $34\leqq m\lt 34+1$ を満たすことがわかります。

解答

トナ：34

解答編　つづき

問題

(iii) 次に、太郎さんと花子さんは、平成28年と令和3年の「通勤・通学」に費やした時間を比較することにした。
　図3は、平成28年の総平均時間、令和3年の総平均時間、平成28年の行動者平均時間、令和3年の行動者平均時間の箱ひげ図を並べたものである。
　ここで、あるデータにおける最大値から第3四分位数を引いた値を $H$ とする。そして平成28年の総平均時間、令和3年の総平均時間、平成28年の行動者平均時間、令和3年の行動者平均時間における $H$ を、それぞれ $H_1, \ H_2, \ H_3, \ H_4$ とする。

　次の(a)、(b)、(c)は、図3に関する記述である。

• (a) 令和3年の総平均時間の最大値は、令和3年の行動者平均時間の最小値より小さい。
• (b) 平成28年の総平均時間の四分位範囲は、平成28年の行動者平均時間の四分位範囲より小さい。
• (c) 総平均時間と行動者平均時間それぞれの、平成28年と令和3年の $H$ の変化を比較すると、 $\dfrac{H_2}{H_1} \gt \dfrac{H_4}{H_3}$ となる。

　(a)、(b)、(c)の正誤の組合せとして正しいものは $\dBox{ニ}$ である。

$\dbox{ニ}$ の解答群

0: (a) 正　(b) 正　(c) 正
1: (a) 正　(b) 正　(c) 誤
2: (a) 正　(b) 誤　(c) 正
3: (a) 正　(b) 誤　(c) 誤
4: (a) 誤　(b) 正　(c) 正
5: (a) 誤　(b) 正　(c) 誤
6: (a) 誤　(b) 誤　(c) 正
7: (a) 誤　(b) 誤　(c) 誤

解説

(1)(iii)

順番に見ていきます。

(a)について、令和3年の総平均時間の最大値は50より小さく、令和3年の行動者平均時間の最小値は50より大きいので、正しいことがわかります。

(b)について、四分位範囲とは、箱の横幅のことなので、平成28年の総平均時間の四分位範囲は、平均28年の行動者平均時間の四分位範囲より小さいことがわかります。つまり、これも正しいです。

(c)について、 $H_i$ は、箱の右側にあるひげの長さです。 $H_2$ は $H_1$ の半分より短いくらいなので、 $\dfrac{H_2}{H_1}$ は $0.5$ くらいだとがわかります。一方、 $H_4$ は $H_3$ より少し短いくらいなので、 $\dfrac{H_4}{H_3}$ は $1$ に近く、少なくとも $0.5$ よりはだいぶ大きいことがわかります。なので、\[ \frac{H_2}{H_1}\lt\frac{H_4}{H_3} \]だから、間違っていることがわかります。

正、正、誤となります。

解答

ニ：1

解答編　つづき

問題

(2) 太郎さんと花子さんは、令和3年における「通勤・通学」と「移動（通勤・通学を除く）」（以下、「移動」）に関し、それぞれの行動に費やした総平均時間と行動者平均時間の関係について話をしている。

• 通勤の途中で、ふだんの経路を大きくはずれて買い物に行ったり病院に行ったりする人もいるけど、こうした行動は「通勤・通学」ではなく、「移動」になるね。「通勤・通学」に費やした時間が長いほど、「移動」に費やした時間は長いのかな。
• じゃあ、それぞれに費やした時間の関係を調べてみようよ。

　図4と図5は「通勤・通学」と「移動」の総平均時間と行動者平均時間の散布図であり、図中の黒丸は、二つの点が完全に重なっていることを表している。なお、三つ以上の点が完全に重なっていることはない。ただし、図4と図5において、同じアルファベットを付している点は、同じ都道府県であることを表している。

(i) 図5から、「通勤・通学」の行動者平均時間が $60$ 以下で、かつ「移動」の行動者平均時間が $75$ 以下である都道府県の数は $\myBox{ヌ}$ である。

解説

(2)(i)

「通勤・通学」の行動者平均時間と「移動」の行動者平均時間を見るので、図5 を使います。

「通勤・通学」の行動者平均時間が 60以下なので、60 より左の部分を見ればいいです。さらに「移動」の行動者平均時間が 75以下なので、75 より下の部分を見ればよく、白丸が4つあることがわかります。

なので、条件を満たす都道府県の数は 4 だとわかります。

解答

ヌ：4

解答編　つづき

問題

(ii) 図4における四つの点 $\mathrm{A, \ B, \ C, \ D}$ が表す都道府県では、「通勤・通学」の総平均時間が同じ値であるが、図5では「通勤・通学」の行動者平均時間について、点 $\mathrm{A}$ が表す都道府県の値は他の三つのどの都道府県の値よりも大きくなっていることがわかる。このようになるのは、 $\dBox{ネ}$ からである。

$\dbox{ネ}$ については、最も適当なものを、次の 0 ～ 3 のうちから一つ選べ。

0: 点 $\mathrm{A}$ が表す都道府県の「通勤・通学」に費やした時間が $0$ である人数の割合が、他の三つのどの都道府県の割合よりも大きい

1: 点 $\mathrm{A}$ が表す都道府県の「通勤・通学」に費やした時間が $0$ である人数の割合が、他の三つのどの都道府県の割合よりも小さい

2: 点 $\mathrm{A}$ が表す都道府県の「移動」に費やした時間が $0$ である人数の割合が、他の三つのどの都道府県の割合よりも大きい

3: 点 $\mathrm{A}$ が表す都道府県の「移動」に費やした時間が $0$ である人数の割合が、他の三つのどの都道府県の割合よりも小さい

解説

(2)(ii)

問題文にある通り、図4 では、「通勤・通学」の総平均時間が同じ値になっていますが、図5 では、「通勤・通学」の行動平均時間について、点 A が他よりも大きくなっています。

問題文の冒頭にあるように、行動者平均時間は

　「通勤・通学」に費やした時間の合計 ÷ 0でないデータの個数

です。総平均時間が等しいということは、A,B,C,D については、分子は等しいということです。A だけが大きくなるには、分母が小さくなる必要があります。つまり、他の都道府県より、「通勤・通学」に費やした時間が 0 である人数の割合が大きいことがわかります。

解答

ネ：0

解答編　つづき

問題

(iii) 太郎さんと花子さんは、総平均時間と行動者平均時間のそれぞれの相関関係について調べることにした。
　「通勤・通学」と「移動」の総平均時間の相関係数は $0.36$ であった。「通勤・通学」と「移動」の行動者平均時間の相関係数を計算するために、表1のように平均値、標準偏差および共分散を求めた。

表1　「通勤・通学」と「移動」の行動者平均時間の平均値、標準偏差、共分散

	平均値	標準偏差	共分散
「通勤・通学」の行動者平均時間	$71.8$	$11.8$	$64.4$
「移動」の行動者平均時間	$76.6$	$7.9$

　表1を用いると、「通勤・通学」と「移動」の行動者平均時間の相関係数は $\myBox{ノ}$ である。

$\mybox{ノ}$ については、最も適当なものを、次の 0 ～ 7 のうちから一つ選べ。

0: $0.01$
1: $0.21$
2: $0.43$
3: $0.58$
4: $0.69$
5: $0.78$
6: $1.02$
7: $1.45$

解説

(2)(iii)

相関係数は、共分散をそれぞれの標準偏差で割ればいいので
\begin{eqnarray} \frac{64.4}{11.8\cdot 7.9} \end{eqnarray}を計算すればいいです。ざっくり計算すると\[ \frac{64}{12\cdot 8}=\frac{2}{3} \]なので、 4 が適当だとわかります。

解答

ノ：4