京都大学 理学部特色入試 2025年度 第4問 解説
(2024年11月に行われた特色入試の問題です。)
問題編
問題
自然数 $n$ に対して、関数 $f_n(x)$ を次で帰納的に定める。
\begin{eqnarray} f_1(x) &=& \sin(x) \\[5pt] f_n(x) &=& \sin(f_{n-1}(x)) \quad(n=2,3,4,\cdots) \end{eqnarray} また、 $L$ を正の実数とし、\[ f_n(a)-\frac{a}{L}=0 \]を満たす実数 $a$ の個数を $A_{L,n}$ とする。このとき、以下の設問に答えよ。(1) $L\leqq 1$ のとき、 $\displaystyle \lim_{n\to\infty} A_{L,n}$ の値を求めよ。
(2) $L\gt 1$ のとき、 $\displaystyle \lim_{n\to\infty} A_{L,n}$ の値を求めよ。
ただし、 $0$ 以上の実数からなる数列 $\{a_n\}$ が、任意の $n$ に対して $a_{n+1}\leqq a_n$ を満たすとき、数列 $\{a_n\}$ が収束することを用いてもよい。
考え方
どういう関数なのか、考えにくいですが、最終的には傾きが $\frac{1}{L}$ の直線との交点の数を考えればいいので、これが数えられる程度の情報がわかればいいです。原点のまわりでどうなっているかを詳しく調べればいいでしょう。
解答編
問題
自然数 $n$ に対して、関数 $f_n(x)$ を次で帰納的に定める。
\begin{eqnarray} f_1(x) &=& \sin(x) \\[5pt] f_n(x) &=& \sin(f_{n-1}(x)) \quad(n=2,3,4,\cdots) \end{eqnarray} また、 $L$ を正の実数とし、\[ f_n(a)-\frac{a}{L}=0 \]を満たす実数 $a$ の個数を $A_{L,n}$ とする。このとき、以下の設問に答えよ。(1) $L\leqq 1$ のとき、 $\displaystyle \lim_{n\to\infty} A_{L,n}$ の値を求めよ。
解答
(1)
$g_n(x)=f_n(x)-\dfrac{x}{L}$ とする。 $A_{L,n}$ は、 $g_n(x)=0$ の実数解の個数である。
$g_n(0)=0$ が成り立つ。また、 $g_n(x)$ は奇関数なので、 $x\gt 0$ の範囲で、 $g_n(x)=0$ の解を調べることにする。
$|f_n(x)|\leqq 1$ より、 $\left|\frac{x}{L}\right|\leqq 1$ つまり、 $0\lt x\leqq L$ の範囲のみ考えればよい。 $L\leqq 1$ より、 $0\lt x\lt \frac{\pi}{2}$ の範囲を考えれば十分である。( $x\geqq \frac{\pi}{2}$ の範囲には解はない)
以下では、まず、$0\lt x\lt \frac{\pi}{2}$ のときに次が成り立つことを示す。
①:$0\lt f_n'(x)\lt 1$ かつ $0\lt f_n(x)\leqq 1$ が成り立つ。
(i) $n=1$ のとき
\begin{eqnarray}
f_1'(x)=\cos x
\end{eqnarray}より、 $0\lt f_1'(x)\lt 1$ かつ $0\lt f_1(x)\leqq 1$ が成り立つ。
(ii) $n=k$ のとき、 $0\lt f_k'(x)\lt 1$ かつ $0\lt f_k(x)\leqq 1$ が成り立つとすると
\begin{eqnarray}
f_{k+1}'(x)=\cos (f_k(x)) f_k'(x)
\end{eqnarray}より、仮定から $0\lt f_{k+1}'(x)\lt 1$ が成り立つ。狭義単調増加で $f_{k+1}(0)=0$ より、 $0\lt f_{k+1}(x)\leqq 1$ が成り立つ。
よって、すべての自然数 $n$ について、①が成り立つ。
①より
\begin{eqnarray}
g_{n+1}'(x)
&=&
\cos (f_n(x)) f_n'(x)-\frac{1}{L} \\[5pt]
&\lt &
1-\frac{1}{L} \leqq 0
\end{eqnarray}より $g_{n+1}(x)$ は狭義単調減少であり、 $g_{n+1}(0)=0$ より、 $0\lt x\lt \frac{\pi}{2}$ で解をもたない。
以上より、 $g_n(x)=0$ の実数解は $1$ 個なので
$\displaystyle \lim_{n\to\infty} A_{L,n}=1$ …(答)
解答編 つづき
問題
(2) $L\gt 1$ のとき、 $\displaystyle \lim_{n\to\infty} A_{L,n}$ の値を求めよ。
ただし、 $0$ 以上の実数からなる数列 $\{a_n\}$ が、任意の $n$ に対して $a_{n+1}\leqq a_n$ を満たすとき、数列 $\{a_n\}$ が収束することを用いてもよい。
解答
(2)
(1)と同様に、 $g_n(x)=f_n(x)-\frac{x}{L}$ とする。
$0\leqq x\leqq \frac{\pi}{2}$ のとき、 $f_1(x)=\sin (x)$ は狭義単調増加で、 $0\leqq f_1(x)\leqq 1\leqq\frac{\pi}{2}$ である。よって、 $f_2(x)=\sin(f_1(x))$ も狭義単調増加で、 $0\leqq f_2(x)\leqq 1$ である。以下、繰り返すと、$0\leqq x\leqq \dfrac{\pi}{2}$ で $f_n(x)$ は狭義単調増加であることがわかる。同様に、
$\dfrac{\pi}{2}\leqq x\leqq \dfrac{3}{2}\pi$ で狭義単調減少
$\dfrac{3}{2}\pi\leqq x\leqq 2\pi$ で狭義単調増加
であることもわかる。また、 $\sin(x+2\pi)=\sin (x)$ を使うと、 $f_n(x)$ についても $f_n(x+2\pi)=f_n(x)$ が成り立つことがわかる。
以上から、 $f_n(x)$ の最大値は、 $x=\frac{\pi}{2}$ のときの値と一致する。この値を $a_n$ とおく。このとき、 $a_{n+1}=\sin(a_n)$ が成り立つ。
$\angle\mathrm{BOA}$ が鋭角のとき、弧 $\mathrm{AB}$ の長さは、 $\mathrm{B}$ から $\mathrm{OA}$ に下ろした垂線の長さより長い。
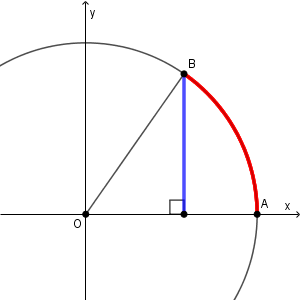
よって、\[a_{n+1}\lt a_n\]が成り立つ。これより、問題文から、数列 $\{a_n\}$ は収束するので、その収束値を $\alpha$ とおく。
\[ a_{n+1}=\sin(a_n) \]に対し、 $n\to\infty$ とすると\[ \alpha=\sin(\alpha) \]が成り立つが、先ほど見たことより、 $0\lt \alpha\lt\frac{\pi}{2}$ のときは $\alpha \gt \sin(\alpha)$ だから、 $\alpha=0$ だとわかる。
よって、 $n$ を十分大きくすれば、\[ a_N\lt \frac{\pi}{2L} \]を満たすものがとれる。 $\{a_n\}$ の単調性から、 $n\gt N$ のとき、\[ a_n\lt \frac{\pi}{2L} \]が成り立つ。このとき、 $x\geqq \frac{\pi}{2}$ の範囲では
\begin{eqnarray}
\frac{x}{L} \geqq \frac{\pi}{2L} \gt a_n \geqq f_n(x)
\end{eqnarray}となり、 $g_n(x)=0$ が解をもたないことがわかる。
以上から、 $n$ が十分大きいときは、 $-\frac{\pi}{2}\lt x\lt \frac{\pi}{2}$ の範囲のみ調べればよい。($n$ を十分大きくすれば、この範囲以外での解が存在しないようにできる)
まず、 $x=0$ のとき、 $g_n(0)=0$ である。また、 $n$ を十分大きくとっているので
\begin{eqnarray}
g_n\left(\frac{\pi}{2}\right)
&=&
a_n - \frac{\pi}{2L} \lt 0
\end{eqnarray}である。
以下では、$0\lt x\lt \frac{\pi}{2}$ のときに次が成り立つことを示す。
\begin{eqnarray} f_n'(0) &=& 1 \\[5pt] f_n'\left(\frac{\pi}{2}\right) &=& 0 \\[5pt] f_n^{\prime\prime}(x) &\lt& 0 \end{eqnarray}これらの式を①とおく。(i) $n=1$ のとき
\begin{eqnarray}
f_1'(x) &=& \cos x \\[5pt]
f_1'(0) &=& 1 \\[5pt]
f_1'\left(\frac{\pi}{2}\right) &=& 0 \\[5pt]
f_1^{\prime\prime}(x) &=& -\sin x
\end{eqnarray}より、①が成り立つ。
(ii) $n=k$ のとき、①が成り立つとすると
\begin{eqnarray}
f_{k+1}'(x) &=& \cos (f_k(x)) f_k'(x) \\[5pt]
f_{k+1}'(0) &=& \cos (f_k(0)) f_k'(0) \\[5pt]
&=& \cos (0) \cdot 1=1 \\[5pt]
f_{k+1}'\left(\frac{\pi}{2}\right)
&=& \cos (f_k\left(\frac{\pi}{2}\right)) f_k'\left(\frac{\pi}{2}\right) \\[5pt]
&=& \cos (f_k\left(\frac{\pi}{2}\right)) \cdot 0=0 \\[5pt]
f_{k+1}^{\prime\prime}(x)
&=&
-\sin (f_k(x)) f_k'(x) \cdot f_k'(x)
+\cos (f_k(x)) f_k^{\prime\prime}(x) \\[5pt]
&=&
-\sin (f_k(x)) \{f_k'(x)\}^2
+\cos (f_k(x)) f_k^{\prime\prime}(x) \\[5pt]
&\lt& 0
\end{eqnarray}が成り立つので、このときも①が成り立つ。
よって、すべての自然数 $n$ について、①が成り立つ。
①より、
\begin{eqnarray}
g_{n}'(0)
&=&
f_{n}'(0)-\frac{1}{L} \\[5pt]
&= &
1-\frac{1}{L} \gt 0 \\[5pt]
g_{n}'\left(\frac{\pi}{2}\right)
&=&
f_{n}'\left(\frac{\pi}{2}\right)-\frac{1}{L} \\[5pt]
&= &
0-\frac{1}{L} \lt 0 \\[5pt]
g_{n}^{\prime\prime}(x) &\lt& 0
\end{eqnarray}となる。
よって、 $0\lt x\lt \frac{\pi}{2}$ で $g_{n}'(x)$ は狭義単調減少なので、 $g_{n}'(b)=0$ となる $b$ ( $0\lt b\lt \frac{\pi}{2}$ )が1つだけ存在する。
・$g_{n}(0)=0$
・$0\lt x\lt b$ で $g_{n}(x)$ が狭義単調増加であること
・$b\lt x\lt \frac{\pi}{2}$ で $g_{n}(x)$ が狭義単調減少であること
・$g_{n}\left(\frac{\pi}{2}\right)\lt 0$
より、 $0\lt x\lt \frac{\pi}{2}$ の範囲で、 $g_{n}(x)=0$ となる解が1つだけ存在する。
以上から、 $n$ が十分大きいとき、 $g_n(x)=0$ の解は、 $x=0$ と正の解、負の解を1つずつもつので、
$\displaystyle \lim_{n\to\infty} A_{L,n}=3$ …(答)
解説
$\sin$ をどんどん合成していく、という少し考えづらい関数ですが、グラフの形はざっくりわかればいいです。
単位円で考えるとわかりやすいですが、 $0$ から $\frac{\pi}{2}$ へ変化させると $\sin x$ は $0$ から $1$ へ変化します。 $1$ ラジアンはだいたい $60^{\circ}$ なので、 $0$ から $1$ へ変化させると、 $\sin x$ は $0$ から $\sin 1$ へ変化します(単調増加)。 $\sin 1$ は $1$ より小さいので、動く範囲はどんどん狭くなっていくことがわかります。
他の範囲も同じように考えると、 $f_n(x)$ の増減と $\sin x$ の増減は連動することがわかります。ただ、値域の幅はどんどん狭くなっていきます。また、周期性があることや奇関数であることもわかります。
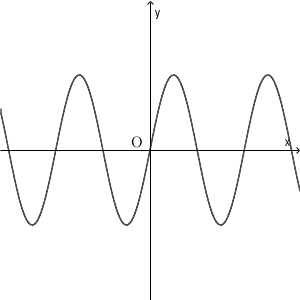
(上の図は、 $y$ 軸方向に圧縮した、 $y=\sin x$ のグラフ)
なので、ざっくりいうと、 $y=\sin x$ のグラフがどんどん $x$ 軸に近づくように縮小されていくイメージです。
しかも、 $f_n'(0)=1$ であることがわかるので、直線 $y=ax$ との交点は $a\geqq 1$ のときは原点だけであることがわかります。(これが (1)のケースです)
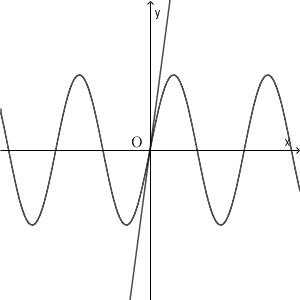
$a\lt 1$ のケースは少し難しいですが、傾きがすごく小さいとき((2)のときです)は、 $y=\sin x$ との交点はたくさんあるかもしれません。

(上の図は、さらに $y$ 軸方向に圧縮した、 $y=\sin x$ のグラフ)
ただ、何度も $\sin x$ を合成していくと、上下の幅はどんどん小さくなり、交点の数は少なくなっていきます。

(上の図は、先ほどの図と同じ縮尺で、 $y=f_{10}(x)$ のグラフをかいたもの)
実際のグラフがかけなくても、増減が $\sin (x)$ のときと同じで、上下の幅が狭くなっていくことがわかれば、交点はどんどん減っていくと予想できます。
$n$ をどんどん大きくしていくと、上下の幅はさらに狭まり、やがて $x=\frac{\pi}{2}$ のときの山頂が直線より下にくるようにできます。そうすると、 $x\gt \frac{\pi}{2}$ では交点はありません。
問題は $0\lt x\lt\frac{\pi}{2}$ の部分ですが、どこまでいっても $f_n'(0)$ は $1$ なので、 $y=f_n(x)$ は、原点のすぐ近くでは直線より上にいるから、少なくとも交点はできます。さらに、グラフの形から、2個以上はないので、結局、 $n$ を大きくしていくと、交点は3つになることがわかります。
このイメージをちゃんと書いたものが上の解答です。
ヒントを見ると、「どんどん減っていくもの」を利用するとわかるので、グラフの上下の幅のところで使います。





