京都大学 理学部特色入試 2025年度 第3問 解説

（2024年11月に行われた特色入試の問題です。）

問題編

問題

　座標平面における領域\[ A=\{(x,y)\mid y\geqq e^x\} \]で定まる図形 $A$ を考える。 $A$ に対して、原点を中心とする回転や平行移動を、何回か行って得られる図形を $n$ 個用意し、それぞれ $A_1,A_2,\cdots,A_n$ とする。
　このとき、 $A_1,A_2,\cdots,A_n$ により座標平面全体を覆うことのできる $n$ の最小値を求めよ。

考え方

4個で覆えるのはすぐに思いつくので、3個の場合がどうなるかを考えるのがメインの問題です。3個でいけるなら具体的に覆い方をいえばいいですが、ダメならどうやってそれを示すが問題になります。こうやればいいという典型的な手法はないので、自分で編み出すしかありません。

解答編

問題

　座標平面における領域\[ A=\{(x,y)\mid y\geqq e^x\} \]で定まる図形 $A$ を考える。 $A$ に対して、原点を中心とする回転や平行移動を、何回か行って得られる図形を $n$ 個用意し、それぞれ $A_1,A_2,\cdots,A_n$ とする。
　このとき、 $A_1,A_2,\cdots,A_n$ により座標平面全体を覆うことのできる $n$ の最小値を求めよ。

解答

$A$ を $y$ 軸方向に $-1$ だけ移動したものを $A_1$ とする。つまり、\[ A_1=\{(x,y)\mid y\geqq e^x-1\} \]とする。

このとき、 $x\leqq 0$ かつ $y\geqq 0$ の領域は $A_1$ に含まれる。よって、 $A_1$ を原点を中心として、反時計回りに $90^{\circ}, 180^{\circ}, 270^{\circ}$ 回転したものをそれぞれ $A_2,A_3,A_4$ とすると、これら4つで座標平面全体を覆うことができる。よって、求める最小値は $4$ 以下である。

以下では、 $n=3$ では座標平面全体を覆うことができないことを示す。原点を中心とした半径 $M$ の円（内側を含む）を $S_M$ とする。どんな $A_1,A_2,A_3$ をとってきても、 $M$ を十分大きくすれば $S_M$ を覆えないようにできることを示す。

$A_1$ を原点を中心に回転し、漸近線が $x$ 軸と平行で、漸近線より上の領域に $A_1$ が含まれるようにする。これを $A_1'$ とおく。

$A$ 内の点 $(0,1)$ が $A_1'$ 内の $(a,b)$ に対応しているとする。このとき、 $A_1'$ の境界線の曲線の方程式は\[ y=e^{x-a}+b-1 \]である。

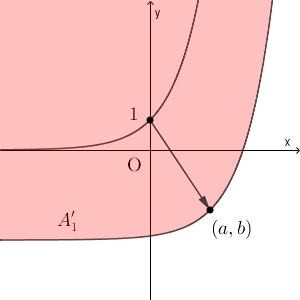
このとき、 $M$ を十分大きくして、 $(a, b)$ が $S_M$ に含まれるようにする。 $A_1'$ と $S_M$ との共通部分を $B_1$ とおく。 $(a,b)$ が第4象限にないときは $(a,b)$ が $(|a|,-|b|)$ に移るように平行移動したほうが、 $S_M$ との共通部分は大きくなるので、 $a\geqq 0$, $b\leqq 0$ としてよい。

$B_1$ のうち、 $x$ 軸より下の部分の面積は\[ 2M(1+|b|) \]以下となる（漸近線が $y=-1-|b|$ だから）。

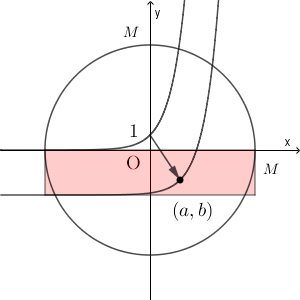
また、 $y=e^{x-a}+b-1$ と $y=M$ との交点の $x$ 座標は
\begin{eqnarray} e^{x-a}+b-1 &=& M \\[5pt] e^{x-a} &=& M-b+1 \\[5pt] x-a &=& \log(M-b+1) \\[5pt] x &=& a+\log(M-b+1) \\[5pt] \end{eqnarray}となるので、 $B_1$ のうち、第1象限内の部分の面積は\[ M(a+\log(M-b+1)) \]以下である。

よって、$B_1$ の面積は次の値以下である。
\begin{eqnarray} \frac{\pi M^2}{4} +M(a+\log(M-b+1)) +2M(1+|b|) \end{eqnarray}ここで \begin{eqnarray} \lim_{M\to\infty} \frac{\frac{\pi M^2}{4} +M(a+\log(M-b+1)) +2M(1+|b|)}{\pi M^2}=\frac{1}{4} \end{eqnarray}なので、 $M$ を十分大きくすれば、$B_1$ の面積を $S_M$ の面積の $\frac{1}{3}$ 未満にできる。よって、$S_M$ と $A_1$ との共通部分の面積も $S_M$ の面積の $\frac{1}{3}$ 未満にできる。

$A_2,A_3$ についても同様のことが言えるので、 $M$ を十分大きくすれば、

　・$A_1$ と $S_M$ との共通部分
　・$A_2$ と $S_M$ との共通部分
　・$A_3$ と $S_M$ との共通部分

これら3つの領域の面積を足しても、 $S_M$ の面積未満とすることができ、 $S_M$ を覆えないので、$A_1,A_2,A_3$ をどのようにとっても、座標平面全体を覆うことはできないことがわかる。

以上より、求める最小値は $4$ …（答）

解説

僕らは、普段こういう感じの領域をかいて、数学の問題を考えています。

この視点を少し変えて、ものすごく遠くからこの領域を見ると、次のようになっています。

$y$ 座標が $M$ のときの $x$ 座標は $\log M$ なので、上の方はそんなに第1象限に食い込んでいかないんですね。イメージでいうと、第2象限を少し膨らませたくらいの大きさでしかなく、この図をイメージできれば、どう考えても3個では覆えないことがわかります。

上の解答では、大きな円を考えると、その 1/4 くらいしか覆えず、円を覆えないなら平面全体も無理でしょう、という流れで示しています。どうやっても隙間が生まれてしまうことを言うために、面積で考えています。厳密な計算は不要で、計算しやすい部分の面積を使えばいいです。