京都大学 理系 2025年度 第5問 解説
問題編
問題
$\theta$ は実数とする。 $xyz$ 空間の 2点 $\mathrm{A}\left(0,0,\dfrac{\sqrt{2}}{4}\right)$, $\mathrm{P}\left(\cos\theta,\sin\theta,\dfrac{1}{2}\cos\theta\right)$ を通る直線 $\mathrm{AP}$ が $xy$ 平面と交わるとき、その交点を $\mathrm{Q}$ とする。 $\theta$ が $-\dfrac{\pi}{4} \lt \theta\lt\dfrac{\pi}{4}$ の範囲を動くときの点 $\mathrm{Q}$ の軌跡を求め、その軌跡を $xy$ 平面上に図示せよ。
考え方
まずは、 $\mathrm{Q}$ の座標を $\theta$ を使って表しましょう。 $\theta$ を消すために使えるものは少ないです。ざっくりとした図をかけば、どういう軌跡になるかは予想できるでしょう。あとは頑張って計算です。
解答編
問題
$\theta$ は実数とする。 $xyz$ 空間の 2点 $\mathrm{A}\left(0,0,\dfrac{\sqrt{2}}{4}\right)$, $\mathrm{P}\left(\cos\theta,\sin\theta,\dfrac{1}{2}\cos\theta\right)$ を通る直線 $\mathrm{AP}$ が $xy$ 平面と交わるとき、その交点を $\mathrm{Q}$ とする。 $\theta$ が $-\dfrac{\pi}{4} \lt \theta\lt\dfrac{\pi}{4}$ の範囲を動くときの点 $\mathrm{Q}$ の軌跡を求め、その軌跡を $xy$ 平面上に図示せよ。
解答
直線 $\mathrm{AP}$ 上の点の座標は、実数 $a$ を使って
\begin{eqnarray}
\left(0,0,\dfrac{\sqrt{2}}{4}\right) +a\left\{ \left(\cos\theta,\sin\theta,\dfrac{1}{2}\cos\theta\right) -\left(0,0,\dfrac{\sqrt{2}}{4}\right)\right\}
\end{eqnarray}と書ける。この $z$ 座標が $0$ となるのは
\begin{eqnarray}
\dfrac{\sqrt{2}}{4}+a\left( \dfrac{1}{2}\cos\theta -\dfrac{\sqrt{2}}{4} \right) &=& 0 \\[5pt]
a\left( \dfrac{1}{2}\cos\theta -\dfrac{\sqrt{2}}{4} \right) &=& -\dfrac{\sqrt{2}}{4} \\[5pt]
a\left( 2\cos\theta -\sqrt{2} \right) &=& -\sqrt{2} \\[5pt]
a &=& -\frac{\sqrt{2}}{2\cos\theta -\sqrt{2}} \\[5pt]
&=& \frac{1}{1-\sqrt{2}\cos\theta} \\[5pt]
\end{eqnarray}
のときなので、点 $\mathrm{Q}$ の座標は\[ \left(\frac{\cos\theta}{1-\sqrt{2}\cos\theta}, \frac{\sin\theta}{1-\sqrt{2}\cos\theta}, 0 \right) \]となる。
ここで、 $\mathrm{Q}(x,y,0)$ とすると
\begin{eqnarray}
x^2 &=& \frac{\cos^2\theta}{1-2\sqrt{2}\cos\theta+2\cos^2\theta} \\[5pt]
y^2 &=& \frac{\sin^2\theta}{1-2\sqrt{2}\cos\theta+2\cos^2\theta} \\[5pt]
x &=& \frac{\cos\theta(1-\sqrt{2}\cos\theta)}{(1-\sqrt{2}\cos\theta)^2} \\[5pt]
&=& \frac{\cos\theta-\sqrt{2}\cos^2\theta}{1-2\sqrt{2}\cos\theta+2\cos^2\theta} \\[5pt]
\end{eqnarray}
となることから
\begin{eqnarray}
x^2+y^2 &=& \frac{1}{1-2\sqrt{2}\cos\theta+2\cos^2\theta} \\[5pt]
x+\sqrt{2}x^2 &=& \frac{\cos\theta}{1-2\sqrt{2}\cos\theta+2\cos^2\theta} \\[5pt]
x^2 &=& \frac{\cos^2\theta}{1-2\sqrt{2}\cos\theta+2\cos^2\theta} \\[5pt]
\end{eqnarray}
となるので\[ (x^2+y^2)-2\sqrt{2}(x+\sqrt{2}x^2)+2x^2 \]を計算すると\[ \frac{1-2\sqrt{2}\cos\theta+2\cos^2\theta}{1-2\sqrt{2}\cos\theta+2\cos^2\theta}=1 \]となることがわかる。これを整理すると
\begin{eqnarray}
(x^2+y^2)-2\sqrt{2}(x+\sqrt{2}x^2)+2x^2 &=& 1 \\[5pt]
x^2+y^2-2\sqrt{2}x-4x^2+2x^2 &=& 1 \\[5pt]
-x^2-2\sqrt{2}x+y^2 &=& 1 \\[5pt]
x^2+2\sqrt{2}x-y^2 &=& -1 \\[5pt]
(x+\sqrt{2})^2-y^2 &=& 1 \\[5pt]
\end{eqnarray}
となる。よって、点 $\mathrm{Q}$ は、双曲線 $(x+\sqrt{2})^2-y^2=1$ 上にあることがわかる。
次に、 $x,y$ のとりうる値の範囲を考える。\[ x=\frac{\cos\theta}{1-\sqrt{2}\cos\theta}=\frac{1}{\frac{1}{\cos\theta}-\sqrt{2}} \]であり、 $0\leqq \theta\lt\dfrac{\pi}{4}$ の範囲で、 $\dfrac{1}{\cos\theta}-\sqrt{2}$ は狭義単調増加で、つねに負の値をとりながら連続的に変化し、 $\theta=0$ のときに $1-\sqrt{2}$ で、 $\theta\to\dfrac{\pi}{4}$ のときに $\dfrac{1}{\cos\theta}-\sqrt{2}\to 0$ となる。以上から、 $x$ は $\dfrac{1}{1-\sqrt{2}}=-1-\sqrt{2}$ 以下のすべての実数値をとりうる。
また、\[ y=\frac{\sin\theta}{1-\sqrt{2}\cos\theta} \]より、 $\theta=0$ のとき $y=0$ で、$\theta\to\dfrac{\pi}{4}$ のときに $y\to -\infty$ で、$\theta\to -\dfrac{\pi}{4}$ のときに $y\to \infty$ であり、連続的に値が変化するので、すべての実数値をとりうる。
以上から、点 $\mathrm{Q}$ の軌跡は、双曲線 $(x+\sqrt{2})^2-y^2=1$ の $x\leqq -1-\sqrt{2}$ の部分なので、以下のようになる。
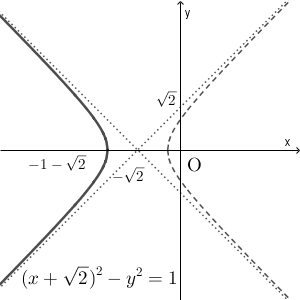
…(答)
解説
上の解答では少し変な計算をしています。 $x^2$ や $y^2$ を計算したときに出てくる分母 $1-2\sqrt{2}\cos\theta+2\cos^2\theta$ と同じものを、分子で作るにはどうすればいいかを考えて、式変形をしています。ただ、本質的な条件式は\[ \sin^2\theta+\cos^2\theta=1 \]です。これが使えるような変形であれば、他の方法でも導くことはできるでしょう。





