京都大学 理系 2024年度 第2問 解説
問題編
問題
$|x|\leqq 2$ を満たす複素数 $x$ と、 $|y-(8+6i)|=3$ を満たす複素数 $y$ に対して、 $z=\dfrac{x+y}{2}$ とする。このような複素数 $z$ が複素数平面において動く領域を図示し、その面積を求めよ。
考え方
動くものが2つあって面倒ですが、 $x,y$ は連動するわけではないので、それぞれ個別に動かして考えましょう。
解答編
問題
$|x|\leqq 2$ を満たす複素数 $x$ と、 $|y-(8+6i)|=3$ を満たす複素数 $y$ に対して、 $z=\dfrac{x+y}{2}$ とする。このような複素数 $z$ が複素数平面において動く領域を図示し、その面積を求めよ。
解答
$x$ は $r(\cos\alpha+i\sin\alpha)$ とかける。ここで、 $r,\alpha$ は、 $0\leqq r\leqq 2$, $0\leqq \alpha\lt 2\pi$ 全体を動く。また、 $y$ は $8+6i+3(\cos\beta+i\sin\beta)$ とかける。ここで、 $\beta$ は $0\leqq \beta\lt2\pi$ 全体を動く。
\begin{eqnarray} z &=& \frac{x+y}{2} \\[5pt] &=& \frac{r}{2}(\cos\alpha+i\sin\alpha)+4+3i+\frac{3}{2}(\cos\beta+i\sin\beta) \\[5pt] \end{eqnarray}と表すことができるので、 $\beta$ を固定して $r,\alpha$ を動かすと、 $z$ は、 $4+3i+\dfrac{3}{2}(\cos\beta+i\sin\beta)$ を中心とする半径 $1$ の円の内部および円周全体を動く。また、この中心 $4+3i+\dfrac{3}{2}(\cos\beta+i\sin\beta)$ は、 $\beta$ を動かすと、 $4+3i$ を中心とする半径 $\dfrac{3}{2}$ の円周全体を動く。この円周を $S$ とおく。
以上より、 $z$ の動く領域は、半径 $1$ の円(内部と円周)を、中心が $S$ にそって動かした領域となる。
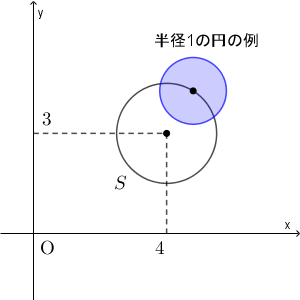
この領域は、 $4+3i$ からの距離が $\dfrac{3}{2}-1=\dfrac{1}{2}$ 以上で $\dfrac{3}{2}+1=\dfrac{5}{2}$ 以下の点全体なので、 $z$ の動く領域は、下の図の色のついた部分である(境界線上の点も含む)。
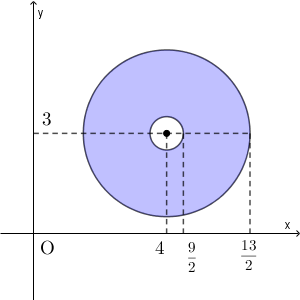
また、面積は\[ \pi\left(\frac{5^2}{2^2}-\frac{1^2}{2^2}\right)=6\pi \]となる。(答)





