京都大学 文系 2025年度 第4問 解説
問題編
問題
座標平面において、曲線 $C_1: y=x^2-2|x|$、曲線 $C_2:y=x^2-5x+\dfrac{7}{4}$、直線 $l_1:x=\dfrac{3}{2}$ を考える。
(1) 点 $(0,0)$ と異なる点で $C_1$ と接し、さらに $C_2$ とも接するような直線 $l_2$ がただ一つ存在することを示せ。
(2) $C_1$ と $l_2$ の共有点を $\mathrm{P}$ とし、その $x$ 座標を $\alpha$ とする。また、 $l_1$ と $l_2$ の共有点を $\mathrm{Q}$ とし、 $C_1$ と $l_1$ の共有点を $\mathrm{R}$ とする。曲線 $C_1$ の $\alpha\leqq x\leqq \dfrac{3}{2}$ の部分、線分 $\mathrm{PQ}$、および線分 $\mathrm{QR}$ で囲まれる図形の面積を求めよ。
考え方
絶対値を含む関数はよく出てきます。場合分けをして考えます。(2)はどの部分の面積を求めるか、図をかいて考えます。(2)では $C_2$ はもはや関係ない点にも注意しましょう。
解答編
問題
座標平面において、曲線 $C_1: y=x^2-2|x|$、曲線 $C_2:y=x^2-5x+\dfrac{7}{4}$、直線 $l_1:x=\dfrac{3}{2}$ を考える。
(1) 点 $(0,0)$ と異なる点で $C_1$ と接し、さらに $C_2$ とも接するような直線 $l_2$ がただ一つ存在することを示せ。
解答
(1)
$f(x)=x^2-5x+\dfrac{7}{4}$ とすると、\[ f'(x)=2x-5 \]なので、 $C_2$ との接点の $x$ 座標が $t$ となる接線の方程式は
\begin{eqnarray}
y
&=&
(2t-5)(x-t)+t^2-5t+\frac{7}{4} \\[5pt]
&=&
(2t-5)x-2t^2+5t+t^2-5t+\frac{7}{4} \\[5pt]
&=&
(2t-5)x-t^2+\frac{7}{4} \\[5pt]
\end{eqnarray}である。
この直線が、 $C_1$ と $x\gt 0$ の部分で接するとする。接線の $x$ 座標を $s$ とすると、 $s\gt 0$ である。 $x\gt 0$ のとき、 $x^2-2|x|=x^2-2x$ なので、 $g(x)=x^2-2x$ とすると\[ g'(x)=2x-2 \]なので、 $(s,g(s))$ での接線の方程式は
\begin{eqnarray}
y
&=&
(2s-2)(x-s)+s^2-2s \\[5pt]
&=&
(2s-2)x-2s^2+2s+s^2-2s \\[5pt]
&=&
(2s-2)x-s^2 \\[5pt]
\end{eqnarray}となるので、係数を比較して
\begin{eqnarray}
\left\{
\begin{array}{l}
2t-5 = 2s-2 \\
-t^2+\dfrac{7}{4} = -s^2
\end{array}
\right.
\end{eqnarray}が成り立つ。ここで、1つ目の式から $t=s+\dfrac{3}{2}$ なので、これを2つ目に代入して
\begin{eqnarray}
\left(s+\frac{3}{2}\right)^2-\frac{7}{4} &=& s^2 \\[5pt]
3s+\frac{9}{4}-\frac{7}{4} &=& 0 \\[5pt]
s &=& -\frac{1}{6} \\[5pt]
\end{eqnarray}となる。しかし、これは $s\gt 0$ を満たさない。つまり、 $C_2$ と接する直線が $C_1$ の $x\gt 0$ の部分で接することはない、とわかる。
次に、 $C_1$ と $x\lt 0$ の部分で接するとする。接線の $x$ 座標を $s$ とすると、 $s\lt 0$ である。 $x\lt 0$ のとき、 $x^2-2|x|=x^2+2x$ なので、 $h(x)=x^2+2x$ とすると\[ h'(x)=2x+2 \]なので、 $(s,h(s))$ での接線の方程式は
\begin{eqnarray}
y
&=&
(2s+2)(x-s)+s^2+2s \\[5pt]
&=&
(2s+2)x-2s^2-2s+s^2+2s \\[5pt]
&=&
(2s+2)x-s^2 \\[5pt]
\end{eqnarray}となるので、係数を比較して
\begin{eqnarray}
\left\{
\begin{array}{l}
2t-5 = 2s+2 \\
-t^2+\dfrac{7}{4} = -s^2
\end{array}
\right.
\end{eqnarray}が成り立つ。ここで、1つ目の式から $t=s+\dfrac{7}{2}$ なので、これを2つ目に代入して
\begin{eqnarray}
\left(s+\frac{7}{2}\right)^2-\frac{7}{4} &=& s^2 \\[5pt]
7s+\frac{49}{4}-\frac{7}{4} &=& 0 \\[5pt]
s+\frac{7}{4}-\frac{1}{4} &=& 0 \\[5pt]
s &=& -\frac{3}{2} \\[5pt]
\end{eqnarray}となる。これは $s\lt 0$ を満たす。これを接線の方程式に代入すると
\begin{eqnarray}
y &=& (2s+2)x-s^2 \\[5pt]
&=& -x-\frac{9}{4} \\[5pt]
\end{eqnarray}となる。
以上より、条件を満たす直線は $y=-x-\dfrac{9}{4}$ ただ1つだけ存在することがわかる。(終)
解答編 つづき
問題
(2) $C_1$ と $l_2$ の共有点を $\mathrm{P}$ とし、その $x$ 座標を $\alpha$ とする。また、 $l_1$ と $l_2$ の共有点を $\mathrm{Q}$ とし、 $C_1$ と $l_1$ の共有点を $\mathrm{R}$ とする。曲線 $C_1$ の $\alpha\leqq x\leqq \dfrac{3}{2}$ の部分、線分 $\mathrm{PQ}$、および線分 $\mathrm{QR}$ で囲まれる図形の面積を求めよ。
解答
(2)
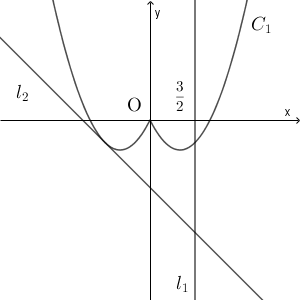
$C_1$ と $l_2$ との共有点の $x$ 座標は
\begin{eqnarray}
x^2+2x &=& -x-\frac{9}{4} \\[5pt]
x^2+3x+\frac{9}{4} &=& 0 \\[5pt]
\left(x+\dfrac{3}{2}\right)^2 &=& 0 \\[5pt]
x &=& -\dfrac{3}{2}
\end{eqnarray}となる。よって、面積は
\begin{eqnarray}
& &
\int_{-\frac{3}{2}}^{0} \left\{(x^2+2x)-\left(-x-\frac{9}{4}\right)\right\} dx \\[5pt]
& &
+\int_0^{\frac{3}{2}} \left\{(x^2-2x)-\left(-x-\frac{9}{4}\right)\right\} dx \\[5pt]
&=&
\int_{-\frac{3}{2}}^0 \left(x^2+3x+\frac{9}{4}\right) dx \\[5pt]
& &
+\int_0^{\frac{3}{2}} \left(x^2-x+\frac{9}{4}\right) dx \\[5pt]
&=&
\left[ \frac{1}{3}x^3+\frac{3}{2}x^2+\frac{9}{4}x \right]_{-\frac{3}{2}}^0 +\left[ \frac{1}{3}x^3-\frac{1}{2}x^2+\frac{9}{4}x \right]_0^{\frac{3}{2}} \\[5pt]
&=&
\left( -\frac{1}{3}\cdot\frac{-27}{8} -\frac{3}{2}\cdot\frac{9}{4} -\frac{9}{4}\cdot \frac{-3}{2} \right) \\[5pt]
& &
+\left( \frac{1}{3}\cdot\frac{27}{8}-\frac{1}{2}\cdot\frac{9}{4}+\frac{9}{4}\cdot \frac{3}{2} \right) \\[5pt]
&=&
\frac{9}{8} -\frac{27}{8}+\frac{27}{8} +\frac{9}{8}-\frac{9}{8} +\frac{27}{8} \\[5pt]
&=&
\frac{9}{2} \\[5pt]
\end{eqnarray}と求められる。(答)





