京都大学 文系 2025年度 第2問 解説
問題編
問題
実数 $a,b$ についての次の条件(*)を考える。
(*) ある実数係数の2次式 $f(x)$ と、ある実数 $c$ に対して、 $x$ についての恒等式\[ \dfrac{1}{8}x^4+ax^3+bx^2=f(f(x))+c \]が成り立つ。
この条件(*) を満たす点 $(a,b)$ 全体の集合を座標平面上に図示せよ。
考え方
「恒等式」と言われたら、やることは限られます。 $f$ の中に $f$ がある、という見た目は文系の人には抵抗があるかもしれませんが、計算を頑張るだけです。
解答編
問題
実数 $a,b$ についての次の条件(*)を考える。
(*) ある実数係数の2次式 $f(x)$ と、ある実数 $c$ に対して、 $x$ についての恒等式\[ \dfrac{1}{8}x^4+ax^3+bx^2=f(f(x))+c \]が成り立つ。
この条件(*) を満たす点 $(a,b)$ 全体の集合を座標平面上に図示せよ。
解答
$f(x)=px^2+qx+r$ とする($p,q,r$ は実数)。このとき、
\begin{eqnarray}
& &
f(f(x)) \\[5pt]
&=&
p(px^2+qx+r)^2+q(px^2+qx+r)+r \\[5pt]
&=&
p(p^2x^4+q^2x^2+r^2+2pqx^3+2prx^2+2qrx) \\[5pt]
& & +pqx^2+q^2x+qr+r \\[5pt]
&=&
p^3 x^4
+2p^2q x^3
+(pq^2+2p^2r+pq)x^2 \\[5pt]
& &
+(2pqr+q^2)x
+(pr^2+qr+r)
\end{eqnarray}となるので、(*)の条件式の両辺の定数項以外の係数を比較すると
\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{1}{8}=p^3 \\[5pt]
a = 2p^2q \\[5pt]
b = pq^2+2p^2r+pq \\[5pt]
0 = 2pqr+q^2 \\[5pt]
\end{array}
\right.
\end{eqnarray}となる。 $p$ は実数なので、1つ目の式から $p=\dfrac{1}{2}$ が得られる。これを代入すると、2つ目から4つ目の式は次のようになる。
\begin{eqnarray}
\left\{
\begin{array}{l}
a = \dfrac{q}{2} \\[5pt]
b = \dfrac{q^2+r+q}{2} \\[5pt]
0 = qr+q^2 \\[5pt]
\end{array}
\right.
\end{eqnarray}となる。3つ目の式から、 $q(r+q)=0$ なので、 $q=0$ または $r=-q$ が成り立つ。
$q=0$ のとき、
\begin{eqnarray}
\left\{
\begin{array}{l}
a = 0 \\[5pt]
b = \dfrac{r}{2} \\[5pt]
\end{array}
\right.
\end{eqnarray}となる。 $r$ は任意の実数なので、 $b$ は実数全体を動く。
一方、 $r=-q$ のときは
\begin{eqnarray}
\left\{
\begin{array}{l}
a = \dfrac{q}{2} \\[5pt]
b = \dfrac{q^2}{2} \\[5pt]
\end{array}
\right.
\end{eqnarray}となる。 $q=2a$ なので、\[ b=\dfrac{(2a)^2}{2}=2a^2 \]が成り立つ。 $q$ は任意の実数なので、 $a$ は実数全体を動く。
以上から、条件(*)を満たす点 $(a,b)$ 全体の集合は、下の図の赤太線部分。
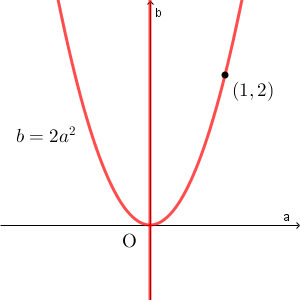
(答)





