🏠 Home / 数学II / 図形と方程式 / 直線と方程式

【標準】ある直線に関して対称な点の座標

🕒 2017/07/28 🔄 2023/05/01

ここでは、ある直線に関して、ある点と対称な点の座標を求める問題を見ていきます。

📘 目次

ある直線に関して対称な点の座標

例題

直線 $l:\ y=2x+1$ に関し、点 $\mathrm{ A }(3,4)$ と対称な点 B の座標を求めなさい。

B の座標を $(p,q)$ とおきましょう。このとき、直線 l と AB との関係を考えて、 B の座標に関する条件式を導きましょう。

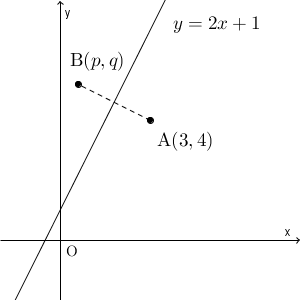
まず、対称であることから、直線 l と A との距離と、直線 l と B との距離は同じです。

ただ、点と直線との距離を求めるのは大変です。それよりも、もっとシンプルに「AB の中点が、直線 l の上にある」と考えたほうが、計算は簡単になります。

【標準】中点の座標で見たように、中点の座標は\[ \left(\frac{3+p}{2}, \frac{4+q}{2}\right) \]なので、これが直線 $l:\ y=2x+1$ 上にあるという条件から、
\begin{eqnarray} \frac{4+q}{2} &=& 2\cdot \frac{3+p}{2}+1 \\[5pt] 4+q &=& 6+2p+2 \\[5pt] q &=& 2p+4 \\[5pt] \end{eqnarray}が得られます。

しかし、点 A との中点が l 上に来るような点はたくさんあります。

上の図のように、青い線上にある点は、点 A との中点が l 上に来るので、中点に関する情報だけでは B を特定することができません。特定するためには、もう1つ条件が必要です。

図を見れば、対称であることから、 l と AB が垂直に交わるという条件が使えることがわかります。垂直に交わるということは、【基本】垂直な直線の方程式で見た内容から、傾きの積が $-1$ になるということですね。このことから、線分 AB の傾きに関する条件を考えて
\begin{eqnarray} \frac{q-4}{p-3} &=& -\frac{1}{2} \\[5pt] 2(q-4) &=& -(p-3) \\[5pt] 2q-8 &=& -p+3 \\[5pt] p+2q-11 &=& 0 \\[5pt] \end{eqnarray}が成り立つことがわかります。

2つの条件式が得られたので、あとは連立方程式を解くだけです。1つ目の条件式を2つ目の条件式に代入して
\begin{eqnarray} p+2(2p+4)-11 &=& 0 \\[5pt] p+4p+8-11 &=& 0 \\[5pt] p &=& \frac{3}{5} \\[5pt] \end{eqnarray}が得られ、これを1つ目の式に代入すれば \begin{eqnarray} q &=& 2p+4 \\[5pt] &=& 2\cdot \frac{3}{5}+4 \\[5pt] &=& \frac{26}{5} \\[5pt] \end{eqnarray}が得られます。

よって、 B の座標は\[ \left(\frac{3}{5}, \frac{26}{5}\right) \]と求めることができます。これが答えです。

このように、「ある直線に関し、ある点と対称な点の座標」を求めるには、中点に着目した条件と傾きに着目した条件の2つを考えます。これらを使えば対称な点を特定することができるし、それほど複雑ではない式が出てくるので、考えやすいでしょう。