🏠 Home / 数学A / 場合の数と確率 / 組合せ

【標準】最短経路の数

🕒 2017/02/16 🔄 2023/05/01

ここでは、最短経路の総数を数える問題を考えます。「組合せ」とどういうふうに関係するか、見ていきましょう。

📘 目次

最短経路の数

例題1

線の上を通って、AからBへ最短で移動する方法は、何通りあるか。

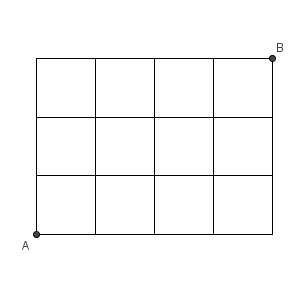
最短経路を1個1個数えていくのは大変ですね。重複や漏れが発生しそうです。

「最短経路」ということは、左や下には行かないということですね。移動する方向は、右か上しかありません。また、どのように移動しても、右に移動する回数は全部で4回、上に移動する回数は全部で3回になるはずです。例えば、「右右上上右右上」と動けばAからBに移動できますが、右が4回、上が3回となっていますね。どこで右かどこで上かは違いますが、右4回・上3回であることは変わりません。そして、移動回数は、つねに7回となります。

このことから、AからBまで移動する7回のうち、右に移動する4回を選べば、それが最短経路と対応することがわかります。もし、「１・２・５・６回目が右」だとすれば、「右右上上右右上」という経路に対応する、ということです。最短経路を直接数えるのは大変ですが、「7回から4回を選ぶ」なら簡単に計算できて\[ {}_7 \mathrm{ C }_4 = \frac{7\cdot 6 \cdot 5 \cdot 4}{ 4\cdot 3 \cdot 2 \cdot 1 } =35 \]通り、と計算できます。もちろん、「上に移動する3回を選ぶ」と考えても答えは同じで、\[ {}_7 \mathrm{ C }_3 = \frac{7\cdot 6 \cdot 5}{ 3 \cdot 2 \cdot 1 } =35 \]通りです。【標準】組合せ#残す方法で見たように\[ {}_n \mathrm{ C }_r={}_n \mathrm{ C }_{n-r} \]であることからもわかります。

途中の点を通る場合

例題2

線の上を通り、AからCを経由してBへ最短で移動する方法は、何通りあるか。

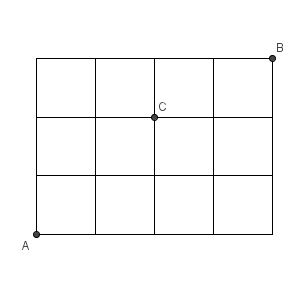
まずAからCに行く方法を考え、次にCからBに行く方法を考えます。「A⇒C」のそれぞれの経路に対して「C⇒B」の経路があるので、2つの経路の総数を掛ければ答えになります。【基本】樹形図と積の法則で見た、積の法則ですね。

AからCへは、4回移動するうち、右に移動する2回を選べばいいですね。一方、CからBへは、3回移動するうち、右に移動する2階を選べばいいです。よって
\begin{eqnarray} {}_4 \mathrm{ C }_2 \times {}_3 \mathrm{ C }_2 = 6\times3=18 \end{eqnarray}通り、となります。

ゴール直前の状況について

目的地に着く直前に注目してみましょう。

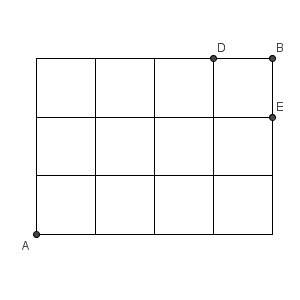
AからBに行く最短経路について考えます。上のようにDとEをとると、最短経路は必ずDかEのどちらかを通らないといけません。また、両方通ることはありません。なので、AからBに行く方法の総数は、AからDに行く方法の総数とAからEに行く方法の総数を足したものになります。【基本】樹形図と和の法則で見た、和の法則です。

Dに行く方法は、6回移動するうち、右に移動する3回を選ぶので ${}_6 \mathrm{ C }_3$ 通り。Eに行く方法は、6回移動するうち、右に移動する4回を選ぶので ${}_6 \mathrm{ C }_4$ 通りです。これを足すと
\begin{eqnarray} {}_6 \mathrm{ C }_3+{}_6 \mathrm{ C }_4=20+15=35 \end{eqnarray}となり、例題1で求めた結果と同じになっていますね。

これを一般的な状況で考えてみましょう。AからBへ最短経路で行くときに n 回の移動が必要だったとします。そのうち、右へ r 回移動しないといけなかったとしましょう。

Bに移動するには、左の点から右に移動するか（上の図のDに対応）、下の点から上に移動してくるか（上の図のEに対応）、どちらかしかありません。左の点から移動してくる場合、Aからその点への移動の仕方は何通りあるでしょうか。まず、移動回数は全体で $n-1$ 回になります。また、Bに行くのに右へ r 回必要なのだから、Bの左の点へは $r-1$ 回、右に移動しないといけません。

一方、AからBの下の点への移動の仕方は、 $n-1$ 回の移動のうち r 回右に行けばいいですね。

この2つを合わせると\[ {}_n \mathrm{ C }_r = {}_{n-1} \mathrm{ C }_{r-1} + {}_{n-1} \mathrm{ C }_r \]が成り立つことがわかります。これは、【標準】特定の1つに注目した組合せでも出てきた内容です。経路の問題とからめて考えることもできるんですね。