【応用】三次関数の最大・最小（区間が動く）

🕒 2017/11/02 🔄 2023/05/01

ここでは、区間に文字が含まれている三次関数の最大・最小を求める問題を考えます。

📘 目次

区間に文字が含まれている三次関数の最大・最小

例題

三次関数 $f(x)=x^3-6x^2+9x$ の $a\leqq x \leqq a+1$ における最大値を求めなさい。（どこで最大となるかは答えなくてよい）

最大値を求めるので、まずはグラフをかいてみましょう。関数を微分すると
\begin{eqnarray} f'(x) &=& 3x^2-12x+9 \\[5pt] &=& 3(x^2-4x+3) \\[5pt] &=& 3(x-1)(x-3) \\[5pt] \end{eqnarray}なので、 $f'(x)=0$ となるのは $x=1,3$ のときです。そのため、増減表は次のようになります。 \begin{array}{c|ccccc} x & \cdots & 1 & \cdots & 3 & \cdots \\ \hline f'(x) & + & 0 & – & 0 & + \\ \hline f(x) & \nearrow & 4 & \searrow & 0 & \nearrow \end{array}ただ、今考えようとしている区間は $a\leqq x \leqq a+1$ です。この区間が、上の増減表のどの部分を表しているかで、最大値をとる場所が変わってきます。下のグラフを見てみましょう。

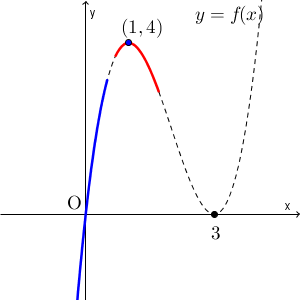
もし、考えている区間が極大値をとるところよりも左にあれば（青い場合）、区間の右端で最大となることがわかります。つまり、 $f(a+1)$ が最大、となります。しかし、極大値をとるところが区間に含まれる場合（赤い場合）は、極大値が最大値となります。つまり、 $f(1)$ が最大ということです。この2つのケースの境目は、区間の右端で極大となるときですね。そうなるのは $a+1=1$ のときだから、 $a=0$ のときです。このことから、 $a\lt 0$ のときは、最大値は $f(a+1)$ であることがわかります。

区間がさらに右に行くと、再び、極大値をとる場所が区間からはずれるようになります（青い場合）。そうなった後は、区間の左端が最大、となります。つまり、最大値は $f(a)$ になる、ということですね。こうなる境目は、区間の左端で極大となるときです。つまり、 $a=1$ のときです。この境目までは、極大値が最大値となります。つまり、 $0\leqq x \leqq 1$ のときは、最大値は $f(1)=4$ となります。

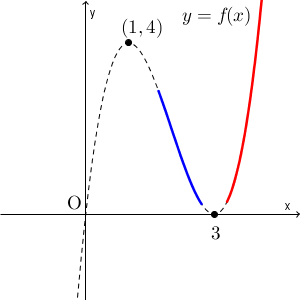
さらに区間が右に動くと、また区間の右端で最大値をとるようになります（赤い場合）。この境目は、区間の左端と右端が同じ値のときです。

こうなるときの $a$ はすぐには求められません。 $f(a)=f(a+1)$ を解く必要があります。

まず、右辺を計算しましょう。
\begin{eqnarray} f(a+1) &=& (a+1)^3-6(a+1)^2+9(a+1) \\[5pt] &=& a^3+3a^2+3a+1 -6a^2-12a-6 +9a+9 \\[5pt] &=& a^3-3a^2+4 \\[5pt] \end{eqnarray}となります。これより、 $f(a+1)-f(a)=0$ となる $a$ は \begin{eqnarray} a^3-3a^2+4 -(a^3-6a^2+9a) &=& 0 \\[5pt] 3a^2-9a+4 &=& 0 \\[5pt] a &=& \frac{9\pm\sqrt{81-48} }{6} \\[5pt] &=& \frac{9\pm\sqrt{33} }{6} \\[5pt] \end{eqnarray}と求められます。答えは2つあります。グラフを見れば、 $f(a)=f(a+1)$ となる点が2つあることがわかります。片方はプラスの方は極小値の近く、もう片方はマイナスの方が極大値の近くです。よって、プラスの方が求めたいものです。

以上から、 $1\lt a \lt \dfrac{9+\sqrt{33} }{6}$ のときは、区間の左端 $f(a)$ が最大、 $a \geqq \dfrac{9+\sqrt{33} }{6}$ のときは、区間の右端 $f(a+1)$ が最大、となります。

以上をまとめると、