🏠 Home / 数学I / 二次関数 / 二次関数の決定

【応用】二次関数の決定（ｘ軸から切り取る長さ）

🕒 2016/09/06 🔄 2023/05/01

ここでは、放物線が x 軸から切り取る線分の長さが与えられている場合に、その二次関数を求める、という問題を考えていきます。なお、他の条件として、頂点の座標も与えられている場合を考えます。

📘 目次

x軸から切り取る線分の長さ

そもそもですが、「放物線が x 軸から切り取る線分の長さ」とはどこを指すのかを確認しておきます。

上の図の、赤い太線の部分の長さが、「放物線が x 軸から切り取る線分の長さ」です。

この長さが与えられている場合に、二次関数を求める問題を考えます。

例題

ある二次関数のグラフの頂点が $(3,-2)$ で、グラフが x 軸から切り取る線分の長さが $4$ のとき、この二次関数を求めなさい。

頂点の座標がわかっているので標準形を使うんじゃないか、と考えたいところですが、「グラフが x 軸から切り取る線分の長さ」をどう扱うかが問題ですね。この部分をどう処理するかを考えないと、つまってしまいます。

ここで注目したいのが、放物線の対称性です。放物線は、軸について対称です。今の場合、直線 $x=3$ について対称なんですね。ということは、 x 軸から切り取る部分の中点は $(3,0)$ になることが分かります。

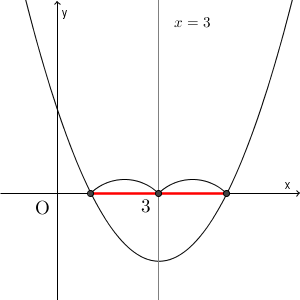
上の図の赤い部分の長さが $4$ で、放物線は左右対称なのだから、実は放物線と x 軸との交点がわかるんですね。 $(1,0)$ と $(5,0)$ です。つまり、【基本】二次関数の決定（x軸との交点指定）のケースに帰着できるわけです。このことから、求める二次関数は次のようにかけることが分かります。\[ y=a(x-1)(x-5) \]この形の方が、標準形より扱いやすいので、こっちをベースに考えます。

求めるのは a だけなので、「この放物線が頂点 $(3,-2)$ を通る」という条件を使って式を１つ作りましょう。
\begin{eqnarray} -2 &=& a(3-1)(3-5) \\ -2 &=& -4a \\ a &=& \frac{1}{2} \\ \end{eqnarray}これから、求める二次関数は\[ y=\frac{1}{2}(x-1)(x-5) \]となることがわかります。