【基本】データの分散

データの散らばりを表すものとして、中央値の考えから派生した四分位数があることを見ました。ここでは、平均値の考えから派生した「分散」という指標を見ていきます。

データの分散

【基本】四分位数で見たヒストグラムをもう一度見てみます。テストの点数と人数との関係を表しています。

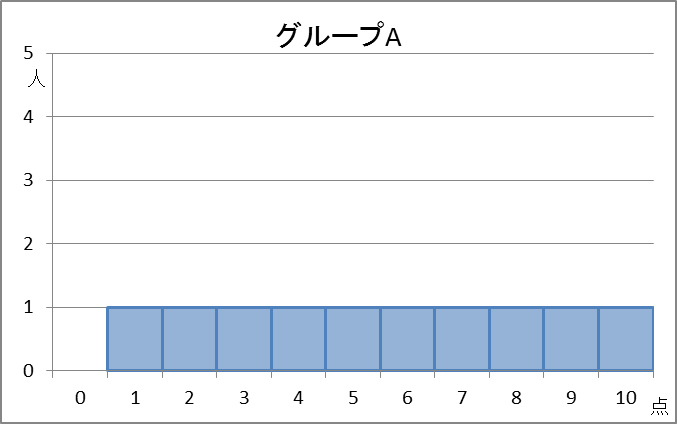
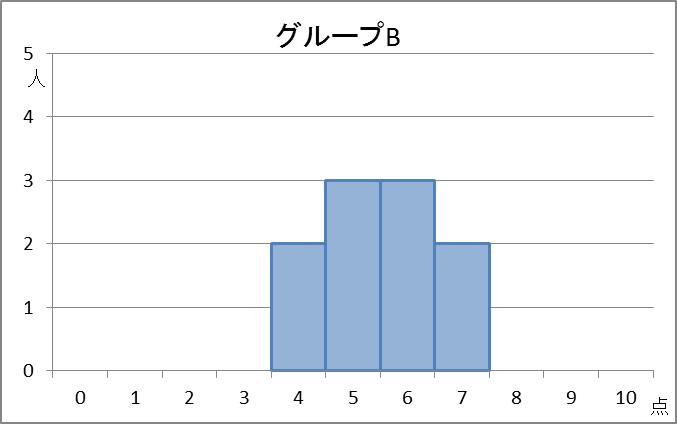
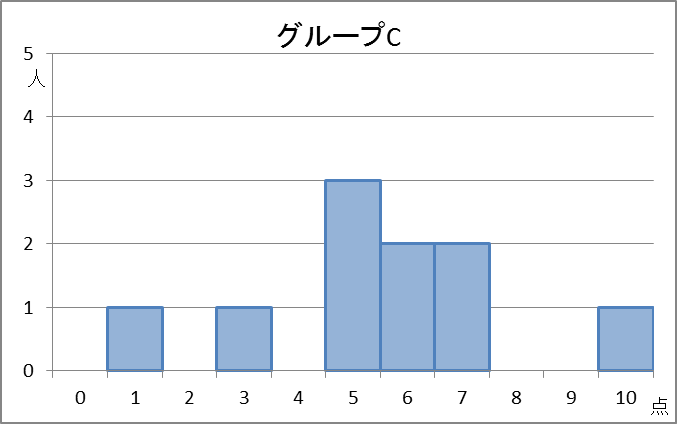
計算してみるとわかりますが、これらの平均値と中央値はともに5.5点です。しかし、データの散らばりは違いますよね。これらを区別するにはどうすればいいでしょうか。

中央値に関しては、四分位数を考えることで、データの散らばりを考えることができました。平均値に関しても、データの散らばりを表す指標があると便利です。

そこでよく使われるのが、分散(variance)というものです。これは、「各数値と平均値との距離」に着目した指標で、次のように計算します。

「平均との差をそれぞれ2乗し、足して個数で割る」ということですね。平均との差が大きくなればなるほど、分散の値は大きくなり、そのとき「データの散らばり具合は大きい」と考えられるので、「分散の大きさは、データの散らばり具合の大きさを表す」と考えられます。

具体的に計算してみましょう。上の例で、グループＡの点数は次のようになっていました。
　Ａ：1,2,3,4,5,6,7,8,9,10
であり、平均値は5.5なので、分散は\[ \frac{4.5^2+3.5^2+2.5^2+1.5^2+0.5^2+0.5^2+1.5^2+2.5^2+3.5^2+4.5^2}{10} = 8.25 \]と計算できます。グループＢの点数は
　Ｂ：4,4,5,5,5,6,6,6,7,7
なので、分散は\[ \frac{1.5^2+1.5^2+0.5^2+0.5^2+0.5^2+0.5^2+0.5^2+0.5^2+1.5^2+1.5^2}{10} = 1.05 \]と計算できます。グループＣの点数は
　Ｃ：1,3,5,5,5,6,6,7,7,10
なので、分散は\[ \frac{4.5^2+2.5^2+0.5^2+0.5^2+0.5^2+0.5^2+0.5^2+1.5^2+1.5^2+4.5^2}{10} = 5.25 \]と計算できます。

以上から、分散は、 $8.25, 1.05, 5.25$ と計算できました。グループＡ、Ｃ、Ｂの順に大きく、グラフから見た散らばり具合の感覚とも一致しています。

標準偏差

分散は、「平均との差をそれぞれ2乗し、足して個数で割る」ことで求められます。ところで、これによって得られる数値の「単位」は何でしょうか。

平均値であれば、数値を足して数値の個数で割っているだけなので、元のデータと同じ単位となります。しかし、分散は二乗しているため、単位が少しおかしくなってしまいます。上の例であれば、「点数の2乗」のようなものになってしまいます。

そのため、分散のルートをとったものを考えることも多いです。これを標準偏差（ひょうじゅんへんさ、standard deviation）といいます。

上の例であれば、グループＡの標準偏差は、$2.872\cdots$ となります。試験に出てくるときには、ルートがきれいに外せるか、小数点第○位まで求めるという形がほとんどです。

なお、「偏差」とは、分散を計算するときに出てきた、「平均値との差」のことをいいます。

おわりに

ここでは、データの散らばりを表す指標である、分散についてみてきました。また、標準偏差についても触れました。

これらは平均値から派生したもので、平均値と同じようにすべての数値が反映されます。そのため、極端な値があると、大きく影響を受けてしまう、といった特徴も同じように持っていることに注意しましょう。