【基本】樹形図と和の法則
ここでは、樹形図の復習をした後で、和の法則を見ていきます。過去に見てきた内容が多く、復習的な要素が強いですが、これから場合の数を考えるうえで重要な考え方なので、ここで紹介しておきます。
樹形図
「〇〇は何通りあるか?」「〇〇はいくつあるか?」という問題を考える場合、「すべてのケースを書き出す」のが基本です。【基本】書き出して数えるでも見ましたが、モレなくダブりなく書き出して数えるようにします。
ただ、毎回、全部を書き出すのは大変です。そこで、同じものを共通にしてかくことのできる、樹形図(tree diagram)を使うことが多いです。【基本】まとめて数えるでも見ましたが、樹形図とは次のような図です。
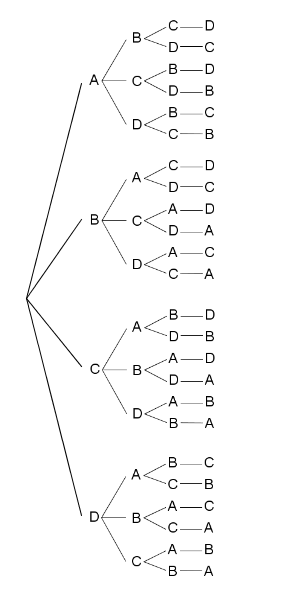
これは、「A, B, C, D を順番に並べる方法は何通りあるか?」を考えるための樹形図です。一番上が「ABCD」という並び順に対応し、一番下が「DCBA」という並び順に対応しています。これを見ると、大きなかたまりが4つあることがわかります。そして、そのかたまりの中に、中くらいのかたまりが3つあります。さらにその中に、2つの場合があります。よって、並べ方の総数は\[ 4\times 3\times 2=24 \]通り、となることがわかります。
慣れてくると、頭の中で樹形図を描き、「1番目が4通りあり、それぞれに2番目をどうするかが3通りあり、さらにそれぞれに3番目と4番目をどうするかが2通りある」と考えて、上のような計算式をスッと出せるようになります。ただ、ベースにあるものは「すべて書き出す」方法であり、樹形図です。
和の法則
次のような例題を考えてみましょう。
まず、大きいサイコロの目が1の場合を考えます。和が4か8になるのは、小さいサイコロの目が3のときだけです。
次に、大が2の場合です。このとき、和が4か8になるのは、小が2の場合と6の場合の2つがあります。先ほどは1通りでしたが、今回は2通りです。
同様に考えていくと、次のようになります(ちょっと書き方を横着しています)。
┏1━3
┣2┳2
┃ ┗6
┣3┳1
┃ ┗5
┣4━4
┣5━3
┗6━2
この結果から、8通りだと求めることができます。
もちろん、こういった解き方でもいいのですが、大きいサイコロの目によって、「和が4か8になるケース」が2つだったり1つだったりして、数え漏れが起こりそうな気もします。
こういう場合に、「ケースを分割して数える」という手法が使えます。今の場合で言うと、「和が4になるケース」と「和が8になるケース」に分け、その2つを後で足す、というやり方です。
和が4になるケースは、次の通りです。
┏1━3
┣2━2
┗3━1
一方、和が8になるケースは次の通りです。
┏2━6
┣3━5
┣4━4
┣5━3
┗6━2
この2つにはダブりがないので、\[ 3+5=8 \]通りと出すことができます。
このように、「かぶらないように場合を分け、それぞれの場合の数を求めて足し合わせる」という手法を使うと、数えやすくなるケースがあります。上の例では、大きいサイコロの目に応じて「和が4か8になる場合」を考えるより、「和が4の場合」「和が8の場合」に分けたほうが、求めやすくなったと思います。書き出したものをチェックする際にも、分けたほうが楽になりますね。
基本は樹形図で考えるのですが、このように樹形図をうまく分割して数えやすくする方法もあるんですね。
この求め方では、和の法則(rule of sum)というものを使っています。特別な名前がついていますが、難しいことはありません。上の内容が分かれば、理解したも同然です。
「同時には起こらないように分ける」「ダブりがないように分ける」という条件はとても大事です。【基本】和集合の要素の個数でも見ましたが、ダブりがある場合は、あとでダブっている部分を引く必要があります。
おわりに
ここでは、和の法則を見ました。ダブりがないようにうまく状況を切り分けることができれば、それぞれのケースを考えて、場合の数を求めることができます。よく使う方法なので覚えておきましょう。





