【基本】四分位数
ここでは、データの散らばりを表す指標として、四分位数を利用したものを考えます。中央値も出てくるので、不安な人は見直しておくと参考になります。
例
別のページで、いろいろなデータの代表値を見てきました。代表値は、データ全体の特徴を表しますが、散らばりまでは表現できません。
例えば、30人の生徒に10点満点のテストをしたとします。この30人を、10人ずつ、グループA・B・Cの3つに分けたとします。テストの結果が、次のようになっていたとしましょう。
A:1,2,3,4,5,6,7,8,9,10
B:4,4,5,5,5,6,6,6,7,7
C:1,3,5,5,5,6,6,7,7,10
こういう場合、数字をただ見るよりも、ヒストグラムなどにしたほうが状況が把握しやすいんでしたね。それぞれ、次のようなグラフになります。
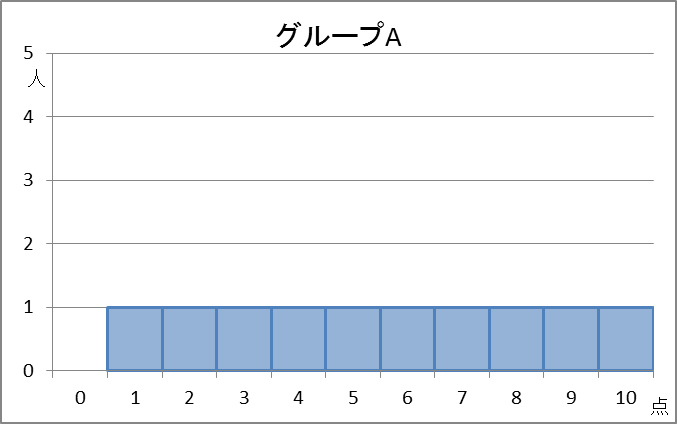
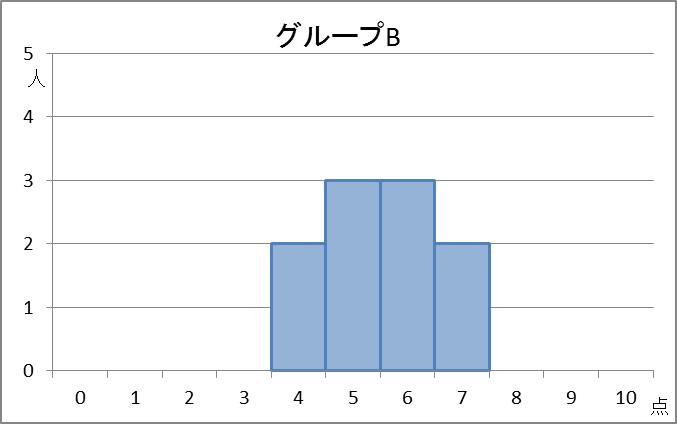
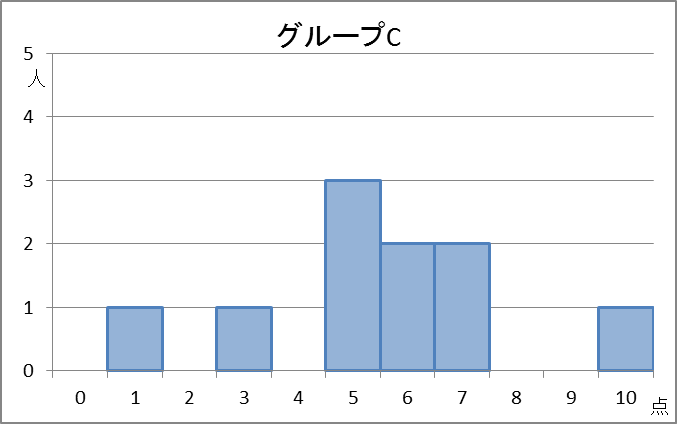
計算してみるとわかりますが、どのグループも、平均値は5.5点、中央値も5.5点となります。つまり、平均値や中央値だけでは、上の3つは区別できません。
でも、散らばりぐらいは違いますよね。グループAは全体に散らばっていますが、グループBは中央に寄っていてあまり散らばっていません。グループCはグループBほど中央に寄っているわけではありませんが、グループAほど散らばっているわけでもありません。
これらを区別する指標があると便利ですよね。
データの範囲
データの散らばりを表す最も基本的なものが、データの範囲(range)です。これは、データの最大値からデータの最小値を引いたものです。一番振れている部分を見て、散らばり具合を把握しよう、という考えです。
グループAもグループCも、最大値は10点、最小値は1点なので、範囲は9点です。グループBは、最大値が7点、最小値が4点なので、範囲は3点です。値が大きいほど散らばっていると考えられるので、データの範囲から「グループAやグループCの散らばり度合いは、グループBの散らばり度合いより大きい」と言えます。
もちろんこの考え方はまずいこともあります。最大値と最小値しか見ていないため、極端に大きすぎる値や小さ過ぎる値が含まれている場合(例えば、天才が試験を受け、ありえない点数をとった場合とか)には、その値だけが反映されてしまいます。このような極端な値が含まれた場合に、その値を見て分析するのは、データの本質からかけ離れてしまいます。
四分位数
データの散らばりを表す上で、「最大値と最小値の差=範囲」を使う場合、極端な値が入っていると困ってしまいます。そこで、データの端から端までではなく、中央付近の範囲をとれば安全なんじゃないか、というアイデアが出てきます。
この発想を利用したものが、四分位数と四分位範囲です。四分位数(しぶんいすう、quartiles)とは、データを大きさの順に並べて4等分したときに、その区切りの位置に来る値のことです。ざっくりいうと、下から25%、50%、75%の値のことです。小さい方から、第1四分位数、第2四分位数、第3四分位数といい、 $Q_1, Q_2, Q_3$ と表すことが多いです。「第2四分位数」というのは、意味を考えればわかりますが、中央値のことです。
そして、第3四分位数と第1四分位数との差、つまり、 $Q_3-Q_1$ のことを、四分位範囲(interquartile range)といいます。「散らばりを表す値」としてよく使われます。この値が大きいほど、散らばっていると考えられるわけですね。
ただ、四分位数を出す上で、少し問題があります。データの数によっては、1/4番目や3/4番目がどこを指すのかわからない、という問題です。
大変ややこしい話なのですが、実は、教科書や人によって求め方が違います。ここでは、その中でも一般的と考えられる決め方を書きます。

まず、データを大きさの順番に並べます。次に、中央値=第2四分位数を先に求めます。データの数が奇数個なら、ちょうど真ん中、偶数個なら、中央の二つの平均で出します(10個なら、5番目と6番目の平均、ということ)。
次に、データを上位と下位に分けます。データが偶数個の場合は、半分半分に分けられます。データが奇数個の場合は、ちょうど真ん中の数値を(1つだけ)除いて、上位と下位に分けます。
そして、第1四分位数は、下位の中央値、第3四分位数は、上位の中央値、とします。
これが一般的な決め方ですが、他にも決め方はあります。定期試験では、授業でやったやり方、教科書に載っているやり方で解きましょう。大学入試では、求め方が指定されているか、指定されていない場合は一般的な方法で求めても同じ答えになるように数値が調整されているはずです。
この定義に沿って計算すると、四分位数は順番に
グループA:3, 5.5, 8
グループB:5, 5.5, 6
グループC:5, 5.5, 7
となり、四分位範囲は、
グループA:5
グループB:1
グループC:2
となります。イメージと合う結果になりましたね。
ちなみに、四分位範囲とほとんど同じ内容ですが、四分位偏差という指標が使われることもあります。四分位偏差は、四分位範囲を2で割ったものです。つまり、 $\displaystyle \frac{Q_3-Q_1}{2}$ です。
おわりに
ここでは、四分位数や四分位範囲について見ました。データの散らばりを見るために使える指標なので、意味をよく理解しておきましょう。





