【基本】双曲線の焦点(焦点がy軸上)
ここでは、焦点が $y$ 軸上にあるときの双曲線について見ていきます。
焦点がy軸上にある双曲線
【基本】双曲線の焦点(焦点がx軸上)とほとんど同じなので、簡略化してみていきます。
点 $(x,y)$ がこの軌跡上にあるとすると、次が成り立ちます。
\begin{eqnarray}
\sqrt{x^2+(y+p)^2}-\sqrt{x^2+(y-p)^2} = \pm 2b
\end{eqnarray}差が $2b$ なので、符号は両方考えられます。以降は、複合同順で考えていきます。
2つ目のルートを右辺に移項し、2乗して整理すると
\begin{eqnarray}
x^2+(y+p)^2 &=& 4b^2 \pm 4b\sqrt{x^2+(y-p)^2}+x^2+(y-p)^2 \\[5pt]
yp-b^2 &=& \pm b\sqrt{x^2+(y-p)^2}
\end{eqnarray}となります。さらに2乗して整理すると
\begin{eqnarray}
-b^2x^2 +(p^2-b^2)y^2 &=& b^2(p^2-b^2) \\[5pt]
\end{eqnarray}となります。ここで、 $p\gt b \gt 0$ なので、 $a=\sqrt{p^2-b^2}$ とおけば、この式は
\begin{eqnarray}
-b^2x^2+a^2y^2 &=& a^2b^2 \\[5pt]
-\frac{x^2}{a^2}+\frac{y^2}{b^2} &=& 1 \\[5pt]
\end{eqnarray}となります。
【基本】双曲線の焦点(焦点がx軸上)と同じようにすれば、この式を満たすすべての点が条件を満たすことがわかります。よって、これが求める軌跡です。
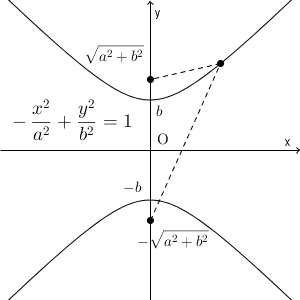
途中で、 $a=\sqrt{p^2-b^2}$ とおきましたが、これを変形すれば $p=\sqrt{a^2+b^2}$ となります。焦点の座標はこれを使って次のように表すことができます。
2つの焦点からの距離の差は $2b$ になります。中心は原点、頂点は $(0,-b)$, $(0,b)$ となります。
焦点がx軸上にある場合とy軸上にある場合
焦点が x 軸にある場合の双曲線は\[ \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2} = 1 \]であり、 y 軸にある場合の双曲線は\[ -\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} = 1 \]となります。どっちがどっちか、わかりにくいと思う人もいるかもしれませんが、特別な点に着目してみましょう。
$x=0$ または $y=0$ となる点を考えてみます。すると、マイナスの符号がついている方が $0$ になるしかないことがわかります。例えば、\[ \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2} = 1 \]の場合、 $y=0$ となることはできますが、 $x=0$ となることはできません。そのため、双曲線は x 軸と交わる、頂点は x 軸上にある、焦点も同じ直線上にあるから x 軸上にある、という流れで覚えておくといいでしょう。
頂点の場所が分かれば、グラフが左右にできるのか、上下にできるのかもわかりますね。わからなくなってしまったときは、特別な点に注目して思い出すようにしましょう。
おわりに
ここでは、焦点が y 軸上にあるときの双曲線の方程式について見ました。また、どちらの軸上にあるかによって、式がどう変わるか、式からどうやって思い出すか、ということも見ました。方程式からどのような双曲線なのか、わかるようになっておきましょう。





