【基本】垂直な直線の方程式
ここでは、垂直な直線の方程式の間には、どのような関係があるかを見ていきます。
垂直な直線の方程式
【基本】平行な直線の方程式では、2つの直線が平行であることと傾きが同じであることが同値であることを見ました。図形の問題では、垂直を扱ったものもたくさんあります。2つの直線が垂直であるときに、その方程式の間にはどのような関係があるかを見ていきましょう。
2つの直線 $y=m_1x+n_1$, $y=m_2x+n_2$ があるとします。これらが垂直に交わっているとき、どういう関係があるかを考えてみましょう。なお、 y 軸に平行な直線を $y=mx+n$ の形で表すことはできないので、どちらの直線も x 軸、 y 軸に平行ではないとします。

まず、この2つの直線が垂直に交わっていることは、切片と何も関係ないことがわかります。 $y=m_1x+n_1$ と $y=m_1x$ とは平行で、 $y=m_2x+n_2$ と $y=m_2x$ とは平行です。そのため、 $y=m_1x+n_1$, $y=m_2x+n_2$ が垂直であることと、 $y=m_1x$, $y=m_2x$ が垂直であることは同値です。切片がない方が考えやすいので、切片がない場合(上の図の青い直線)について考えましょう。
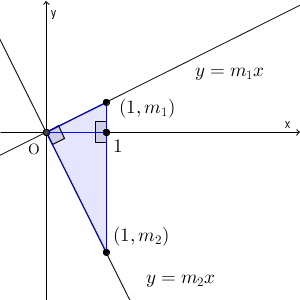
$y=m_1x$, $y=m_2x$ について考えます。この2直線が垂直とします。このとき、 $(1,m_1)$, $(1,m_2)$, $(0,0)$ を結ぶと、直角三角形になります。よって、三平方の定理が成り立ちます。そこで、各辺の長さの2乗を求めてみましょう。
まずは斜辺です。 $(1,m_1)$, $(1,m_2)$ の2点のうち、どちらかは x 軸より上で、どちらかは x 軸より下にあるので、斜辺の2乗は\[ (m_1-m_2)^2 \]となります。なお、 $(m_1+m_2)^2$ ではないことに注意しましょう。上の図であれば、 $m_2$ は負です。そのため、斜辺のうち、 x 軸より下の部分の長さは $-m_2$ になります。マイナスがつくことに注意しましょう。
斜辺以外の2辺の長さの2乗は、 $(1,0)$ へ垂線をおろして考えれば、それぞれ $1+m_1^2$, $1+m_2^2$ となります。
よって、三平方の定理から
\begin{eqnarray}
(m_1-m_2)^2 &=& (1+m_1^2) +(1+m_2^2) \\[5pt]
-2m_1m_2 &=& 2 \\[5pt]
m_1m_2 &=& -1 \\[5pt]
\end{eqnarray}が得られます。よって、2直線が垂直であれば、傾きの積が $-1$ になることがわかります。
逆に、 $m_1m_2=-1$ が成り立つときは、上の式をそのまま逆にたどっていくと\[ (m_1-m_2)^2 = (1+m_1^2) +(1+m_2^2) \]が成り立つことがわかるので、 $y=m_1x$, $y=m_2x$ は垂直に交わることもわかります。よって、 $y=m_1x+n_1$, $y=m_2x+n_2$ も垂直に交わります。
以上のことから、2直線が垂直であることと、直線の方程式における傾きについて、次のことが言えることがわかります。
例えば、「 $y=2x+3$ に垂直な直線の方程式は?」と言われれば、傾きが $-\dfrac{1}{2}$ の直線だ、ということがすぐにわかるんですね。
おわりに
ここでは、2直線が垂直であることと、傾きの積が $-1$ であることが同値であることを見ました。
平行なら傾きは同じ、垂直なら傾きの積が $-1$ 。とてもシンプルですが、今後よく使うようになります。





