【基本】平行な直線の方程式

ここでは、平行な直線の方程式の間には、どのような関係があるかを見ていきます。すでに知っている人もいると思いますが、別のページで取り上げる「垂直に交わる場合」との関連で取り上げます。

平行な直線の方程式

過去に解いたことのある図形の問題を思い出してみると、「平行な2直線」に関する問題をよく見かけたと思います。同位角や錯角を使う問題もあったし、平行四辺形に関する問題などもありましたね。

これらの問題を直線の方程式を使っても解けるようにするためには、「平行な直線に対して、その方程式の間には、どのような関係があるのか」を知っておくと役立ちます。すでに知っている人もいると思いますが、復習の意味も込めてもう一度見てみましょう。

2つの直線 $y=m_1x+n_1$, $y=m_2x+n_2$ があるとします。これらが平行であるときにどういう関係があるかを考えてみましょう。

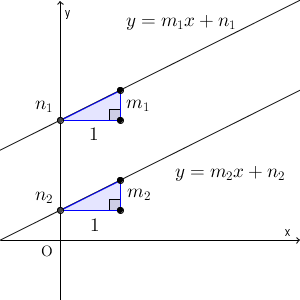
上の図のように $(0,n_1)$, $(1,n_1)$, $(1,m_1+n_1)$ を結びます。また、 $(0,n_2)$, $(1,n_2)$, $(1,m_2+n_2)$ も同様に結びます。 $m_1$ や $m_2$ が $0$ でなければ、直角三角形ができます。

まずは、2直線が x 軸と平行でない場合、つまり、上のように点を結んで直角三角形ができる場合を考えましょう。2直線は平行だから同位角が等しいので、2直線と y 軸とのなす角は同じになります。よって、 x 軸（に平行な直線）とのなす角も等しくなります。

このことから、 x 軸と平行な辺と、その両端の角がそれぞれ等しくなることから、2つの直角三角形は合同になります。よって、 $m_1=m_2$ が成り立ちます。

また、2直線が x 軸と平行な場合は、 $m_1=0$, $m_2=0$ なので、このときも $m_1=m_2$ が成り立ちます。

つまり、2直線が平行であれば、 $m_1=m_2$ が成り立ちます。

逆に、 $m_1=m_2$ だったとします。すると、この2直線が平行になるかどうかを考えてみましょう。

まずは $m_1=m_2\ne0$ とします。 x 軸に平行な辺、 y 軸に平行な辺の長さが等しく、その間の角も直角なので等しいため、2つの直角三角形は合同になります。よって、2直線と y 軸となす角がそれぞれ等しくなることがわかります。同位角が等しいので、2直線は平行です。

$m_1=m_2=0$ の場合は、ともに x 軸と平行だから、やはり2直線は平行です。

以上のことから、2直線が平行であることと、直線の方程式における傾きについて、次のことが言えることがわかります。

x の係数のことが「傾き」を表していることを考えれば、「同じだけ傾いているのだから平行だ」ということは当たり前ですね。

ちなみに、 $m_1=m_2$ が成り立ち、 $n_1=n_2$ も成り立っていたとすると、この2つの直線は一致しています。このときも、「2つの直線は平行である」と考えます。少し変な感じがしますけども。

おわりに

ここでは、2直線が平行であることと、その方程式の傾きが等しくなることが同値であることを見ました。傾きの意味を考えれば、わかりやすい結果ですね。