【基本】平均変化率

🕒 2017/10/02 🔄 2023/05/01

【導入】微分を考える意味についてでは、微分を使えば三次（以上の）関数のグラフがかけるようになる、という話をしました。グラフを描くには、山の部分や谷の部分の情報が必要でしたね。

こうした山の部分や谷の部分は、二次関数のときにもありました。頂点のところです。まずは、二次関数を使って、山や谷の部分について考えてみましょう。

📘 目次

平均変化率

$y=x^2$ という二次関数について考えてみます。グラフは次のようになりますね。

x を小さい値から徐々に増やしていったとしましょう。そうすると、谷底の部分までは y の値は減っていき、底を超えると今度は増えていきます。

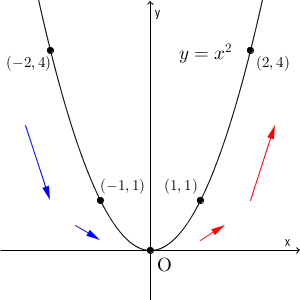
例えば、 $(1,1)$ という点を考えてみましょう。原点からこの点までは x が増えるたびに y が増え、この後も増え続けることがわかります。実際、1つ前と1つ後の点を見れば、 $(0,0)$ と $(2,4)$ なので、 $0⇒1⇒2$ と増えるたびに、 $0⇒1⇒4$ と増えていますね。

一方、 $(-1,0)$ という点を同じように考えてみると、 $-2⇒-1⇒0$ と増えるたびに、 $4⇒1⇒0$ と減っていきます。また、一番重要な谷底の部分である原点 $(0,0)$ は、 x が $-1⇒0⇒1$ と増えると、 $1⇒0⇒1$ と変化します。この「減って増える」という変化が、まさに谷の部分を表しているわけですね。

こうしたことから、 x が変化したときに、 y がどう変化するか、というのが重要であることがわかります。この変化量同士を割ったもの、つまり、「 x の変化量で y の変化量を割ったもの」は、「平均変化率」とよばれ、今後、微分を考える上でキーとなってきます。

平均変化率

x が a から b まで変化するときに、 y が A から B まで変化するとき、次の値を「x が a から b まで変化するの y の平均変化率」という\[ \frac{B-A}{b-a} \]

これは、言い換えれば、 $(a,A)$ と $(b,B)$ を結んだ直線の傾きですね。

なぜ y の変化量そのものではなく、 x の変化量で割ったものを考えるのか、については、いくつか理由があります。

1つは、 x の変化量で割らなければ、他の点での比較が難しい、というのがあります。例えば、 $y=x^2$ で、 x が $1⇒2$, $0⇒2$ と変化したとき、 y の変化は、それぞれ $1⇒4$, $0⇒4$ となります。変化幅だけで見ると、後者の方が大きいですが、それって単純に x の変化幅が大きいからですよね。 x の変化量で割れば、それぞれの傾きが求められ、変化の割合を比べられるようになります。

変化の割合を比較すると、 $\dfrac{4-1}{2-1}=3$, $\dfrac{4-0}{2-0}=2$ であり、前者の方が変化の仕方が急であることがわかります。増えているかどうかだけでなく、増え方が大きいかどうかもわかるわけですね。こうした情報が得られることからも、単純に y の変化幅だけでなく、平均変化率を考えることが重要であることがわかります。

また、 x の変化量で割ることで、 x を増やす変化、減らす変化、どちらでも同じ値になります。 x を $0⇒1$ と変化させたときと $1⇒0$ と変化させたときで、 y の変化量は違いますが、平均変化率は同じです。

他にも、微分について学んでいくと、 y の変化幅ではなく、平均変化率を出発点にしていることの重要性に気づくと思いますが、とりあえずここではこの辺にしておきましょう。

さて、最後に、少しだけ抽象的な計算をしてみましょう。 $y=x^2$ で x が a から b まで変化するとします( $a\ne b$ )。このとき、 y の平均変化率を計算してみましょう。
\begin{eqnarray} \frac{b^2-a^2}{b-a} = \frac{(b-a)(b+a)}{b-a}=b+a \end{eqnarray}となります。うまく $(b-a)$ が出てきたため、最後はきれいな式になりましたね。

この式があれば、 x が $1⇒2$, $0⇒2$ と変化したとき、平均変化率は、それぞれ、 $3$, $2$ となることがすぐにわかります。上で計算したように、対応する y を求めて、変化量の割合を求める、という流れよりも楽に計算できます。