東京大学 理系 2014年度 第1問 解説
問題編
問題
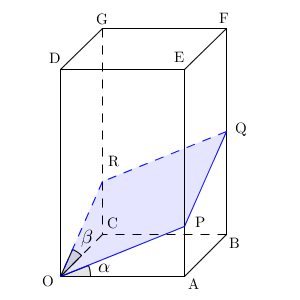
1辺の長さが $1$ の正方形を底面とする四角柱 OABC-DEFG を考える。3点 P, Q, R を、それぞれ辺 AE, 辺 BF, 辺 CG 上に、4点 O, P, Q, R が同一平面上にあるようにとる。四角形 OPQR の面積を S とおく。また、 $\angle \mathrm{ AOP }$ を $\alpha$, $\angle \mathrm{ COR }$ を $\beta$ とおく。
(1) S を $\tan\alpha$ と $\tan\beta$ を用いて表せ。
(2) $\displaystyle \alpha+\beta=\frac{\pi}{4}$, $\displaystyle S=\frac{7}{6}$ であるとき、 $\tan\alpha+\tan\beta$ の値を求めよ。さらに、 $\alpha\leqq \beta$ のとき、 $\tan\alpha$ の値を求めよ。
考え方
(1)は、各点の座標が簡単に出せるので、ベクトルで出てくる三角形の公式を使いましょう。
(2)では、 $\tan\alpha$ を求めるより先に $\tan\alpha+\tan\beta$ を求めなさい、と言われています。これは、「 $\tan\alpha$ を直接求めることはやめましょう」や「 $\tan\alpha+\tan\beta$ をひとかたまりだと思って考えなさい」というヒントです。出題者のやさしさです。これを無視して $\tan\alpha$ を直接求めようとすると、4次方程式が出てきてしまいます。
解答編
問題
1辺の長さが $1$ の正方形を底面とする四角柱 OABC-DEFG を考える。3点 P, Q, R を、それぞれ辺 AE, 辺 BF, 辺 CG 上に、4点 O, P, Q, R が同一平面上にあるようにとる。四角形 OPQR の面積を S とおく。また、 $\angle \mathrm{ AOP }$ を $\alpha$, $\angle \mathrm{ COR }$ を $\beta$ とおく。
(1) S を $\tan\alpha$ と $\tan\beta$ を用いて表せ。
(2) $\displaystyle \alpha+\beta=\frac{\pi}{4}$, $\displaystyle S=\frac{7}{6}$ であるとき、 $\tan\alpha+\tan\beta$ の値を求めよ。さらに、 $\alpha\leqq \beta$ のとき、 $\tan\alpha$ の値を求めよ。
解答
この四角柱は直角柱(各側面が底面と垂直に交わる)とする。
(1) O を原点とし、 A, C の座標をそれぞれ $(1,0,0)$, $(0,1,0)$ とする。また、 D の z座標を正とする。
このとき、 $\overrightarrow{ \mathrm{ OP } }$, $\overrightarrow{ \mathrm{ OR } }$ の成分は、それぞれ $(1,0,\tan\alpha)$, $(0,1,\tan\beta)$ となる。これから、三角形 OPR の面積は
\begin{eqnarray}
& &
\frac{1}{2} \sqrt{ |\overrightarrow{ \mathrm{ OP } }|^2 |\overrightarrow{ \mathrm{ OR } }|^2 -(\overrightarrow{ \mathrm{ OP } } \cdot \overrightarrow{ \mathrm{ OR } })^2 } \\
&=&
\frac{1}{2} \sqrt{(1+\tan^2\alpha)(1+\tan^2\beta) -(\tan\alpha\tan\beta)^2 } \\
&=&
\frac{1}{2} \sqrt{1+\tan^2\alpha+\tan^2\beta } \\
\end{eqnarray}となる。四角形 OPQR は、2組の向かい合う辺がそれぞれ平行なので平行四辺形となるから、この面積 S は三角形 OPR の面積の2倍となる。よって\[ S=\sqrt{1+\tan^2\alpha+\tan^2\beta } \]となる。
(2) (1)と $\displaystyle S=\frac{7}{6}$ より
\begin{eqnarray}
\sqrt{1+\tan^2\alpha+\tan^2\beta } &=& \frac{7}{6} \\[5pt]
1+\tan^2\alpha+\tan^2\beta &=& \frac{49}{36} \\[5pt]
\tan^2\alpha+\tan^2\beta &=& \frac{13}{36} \cdots (X) \\[5pt]
\end{eqnarray}が成り立つ。
また、 $\displaystyle \alpha+\beta=\frac{\pi}{4}$ から
\begin{eqnarray}
\tan\beta
&=&
\tan \left(\frac{\pi}{4} -\alpha\right) \\[5pt]
&=&
\frac{1-\tan\alpha}{1+\tan\alpha} \cdots (Y) \\[5pt]
\end{eqnarray}が成り立つ。これを変形して
\begin{eqnarray}
(1+\tan\alpha)\tan\beta &=& 1-\tan\alpha \\[5pt]
\tan\alpha\tan\beta &=& 1-\tan\alpha-\tan\beta \\[5pt]
\end{eqnarray}が成り立つ。
これを $(X)$ に代入すると
\begin{eqnarray}
(\tan\alpha+\tan\beta)^2 -2\tan\alpha\tan\beta &=& \frac{13}{36} \\[5pt]
(\tan\alpha+\tan\beta)^2 -2(1-\tan\alpha-\tan\beta) &=& \frac{13}{36} \\[5pt]
\end{eqnarray}となる。 $p=\tan\alpha+\tan\beta$ とおけば
\begin{eqnarray}
p^2-2+2p &=&\frac{13}{36} \\[5pt]
36p^2 +72p -85 &=& 0 \\[5pt]
(6p-5)(6p+17) &=& 0 \\[5pt]
\end{eqnarray}が得られる。 $p=\tan\alpha+\tan\beta \gt 0$ なので、 $p=\frac{5}{6}$ と求められる。よって、 $\displaystyle \tan\alpha+\tan\beta=\frac{5}{6}$ である。
この式で $t=\tan\alpha$ とおき、 $(Y)$ を代入すると、
\begin{eqnarray}
t +\frac{1-t}{1+t} &=& \frac{5}{6} \\[5pt]
6t(1+t) +6(1-t) &=& 5(1+t) \\[5pt]
6t^2 -5t +1 &=& 0 \\[5pt]
(3t-1)(2t-1) &=& 0 \\[5pt]
\end{eqnarray}これより、 $\displaystyle t=\frac{1}{3}, \frac{1}{2}$ となる。 $\displaystyle \tan\alpha = \frac{1}{3}$ とすると $\displaystyle \tan\beta = \frac{1}{2}$ となり、 $\displaystyle \tan\alpha = \frac{1}{2}$ とすると $\displaystyle \tan\beta = \frac{1}{3}$ となる。 $\alpha \leqq \beta$ なので、 $\displaystyle \tan\alpha=\frac{1}{3}$ である。
解説
(2)では、「 $\tan\alpha+\tan\beta$ を求めてから $\tan\alpha$ を求めなさい」と言われているので、まずは $\tan\alpha+\tan\beta$ をひとかたまりにして解くのではないか、と考えてみましょう。(1)から得られる式は対称式になっているので、 $x^2+y^2=(x+y)^2-2xy$ という、よくある変形を行います。条件式も使って、 $xy$ にあたる部分を変形すれば、あとは簡単な計算です。この条件式の変形が少し思いつきにくいかもしれませんが。
$(Y)$ の式を $(X)$ に代入して $\tan\alpha$ をいきなり求めようとすると、次のような4次方程式が出てきてしまいます。\[ 36t^4 +72t^3 +59t^2 -98t +23 = 0 \]解けないことはないですが、因数分解はなかなか難しいです。4次方程式を解く方法だと、止まってしまう可能性があります。