京都大学 理学部特色入試 2016年度 第3問 解説
(2015年11月に行われた特色入試の問題です。2016年に行われた特色入試の問題はこちら)
問題編
問題
nを3以上の整数とし、kを自然数とする。表裏の区別のつくn枚のコインを用いて1人で以下のゲームを行う。
- まず、ゲームの初期状態として、n枚のコインを円周上に等間隔に並べる。各コインは表または裏である。
- 以下の操作を何回か繰り返す。 (操作)並べたコインの中から連続するk枚を選び、選んだコインをすべてひっくり返す。
- この操作を何回か行った結果、すべてのコインを表にすることができれば、ゲームは終了する。
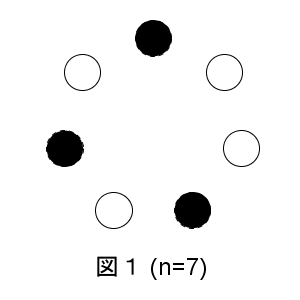
ゲームの初期状態の例(黒丸:コインの表、白丸:コインの裏)
以下の設問に答えよ。
(1) $n=7、k=3$ とする。初期状態が図1のとき、このゲームを終了させることができることを示せ。また、すべてのコインを表にするまでに必要な操作の最小回数を求めよ。
(2) $n=6、k=3$ とする。初期状態が図2のとき、このゲームを終了させることはできないことを示せ。
(3) どのような初期状態であっても必ずこのゲームを終了させることができるための、n、kに関する必要十分条件を求めよ。
考え方
問1は、できるかどうかを考えるだけなら簡単ですね。試行錯誤すれば、何とか答えにたどり着けるはずです。問題はそれが最小であることを示すことです。操作の制限から、「それより少ない回数ではできない」ということを示していきます。
問2は、「終了できないこと」なのでよりハードルが高いです。これも、操作の制限から「できない」ことを示していきます。問3はそれの一般化なので、問2をヒントに解いていきます。
よく考えると、「連続するk個」を2回ひっくり返すと元に戻るので、同じk個のコインを2回以上ひっくり返すことに意味はありません。つまり、1回ひっくり返すかそのままかしかありません。とすると、実は操作は最大でn回しかなく、考えるべき条件はかなり限られます。
解答編
問題
nを3以上の整数とし、kを自然数とする。表裏の区別のつくn枚のコインを用いて1人で以下のゲームを行う。
- まず、ゲームの初期状態として、n枚のコインを円周上に等間隔に並べる。各コインは表または裏である。
- 以下の操作を何回か繰り返す。 (操作)並べたコインの中から連続するk枚を選び、選んだコインをすべてひっくり返す。
- この操作を何回か行った結果、すべてのコインを表にすることができれば、ゲームは終了する。
以下の設問に答えよ。
(1) $n=7、k=3$ とする。初期状態が図1のとき、このゲームを終了させることができることを示せ。また、すべてのコインを表にするまでに必要な操作の最小回数を求めよ。
問題
(1)
一番上のコインを「1」とし、時計回りに7まで数字をふっていく。初期状態は、1と4と6が表である。表を○、裏を×と書くと、コインは順番に「○××○×○×」となっている。
「712」をひっくり返すと、コインは「×○×○×○○」となる。
「123」をひっくり返すと、コインは「○×○○×○○」となる。
「234」をひっくり返すと、コインは「○○×××○○」となる。
「345」をひっくり返すと、コインは「○○○○○○○」となる。
以上から、4回の操作でこのゲームを終了させることができる。
次に、4回未満の操作では、このゲームを終了させることができないことを示す。
操作を繰り返してすべてのコインが表になるには、はじめに表だったコインは偶数回、裏だったコインは奇数回をひっくり返らないといけない。初期状態では、表が3枚、裏が4枚だったので、コインをひっくり返す回数をすべて足し合わせると偶数になる必要がある。1回の操作で3枚裏返すので、操作の回数は偶数でないといけない。
2回の操作ですべて表にできたとする。このとき、どちらかの操作で「1と6」か「4と6」のコインをひっくり返さないといけない。しかし、「1と6」をひっくり返すと、別の1回の操作で「7と4」を同時に表にすることはできす、「4と6」をひっくり返すと、別の1回の操作で「1と5」を同時に表にすることはできない。よって、2回の操作では、すべてを表にすることはできない。
以上から、今の場合、このゲームを終了するのに必要な操作の最小回数は、4回となる。
解答編 つづき
問題
(2) $n=6、k=3$ とする。初期状態が図2のとき、このゲームを終了させることはできないことを示せ。
解説
ちょっと入れ替えると、1枚だけ裏にすることができます。このほうが扱いやすいので、そう変換してから考えます。何度も何度もひっくり返すと混乱してきますが、実は何度もひっくり返すことに意味はありません。同じ場所を2回ひっくり返すと、元に戻ります。また、ひっくり返す順番が変わっても、結果は同じです。なので、それぞれの「連続するk枚」は、1回ひっくり返すかひっくり返さないかだけを考えればよく、2回以上ひっくり返す必要はありません。
今の場合だと、それぞれの「連続する3枚のコイン」を、ひっくり返すかひっくり返さないかを決めていくだけでOKです。それでできなければ、永遠にできません。それぞれひっくり返す回数は最大で3回なので、ひっくり返す回数は限定され、すべて表にはできないことが示せます。
解答
(2)
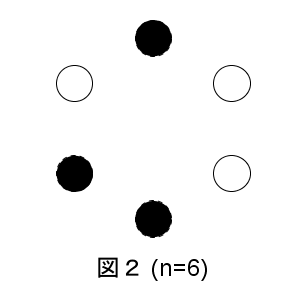
一番上のコインを「1」とし、時計回りに6まで数字をふっていく。初期状態は、1と4と5が表である。表を○、裏を×と書くと、コインは順番に「○××○○×」となっている。
「612」をひっくり返すと、コインは「×○×○○○」となる。
「123」をひっくり返すと、コインは「○×○○○○」となる。
以下では、このように1枚だけ裏の状態から、すべて表の状態にはできないことを示す。
同じ場所に2回「操作」を行うと元に戻る。また、操作の順番は結果に影響しない。よって、すべて表の状態にできるとすると、それぞれの「連続する3枚」について、操作は高々1回しか行わなくてよい。このとき、各コインについて、ひっくり返す回数は最大で3回となる。
一枚だけ裏の状態からすべて表にできたとすると、はじめ裏だったコインは1回か3回裏返る。その両隣の表のコインは、どちらか一枚は裏返る必要がある。コインは最大で3回しか裏返らないので、そのコインは2回裏返ることになる。また、そのコインが2回裏返るためには、「連続する3枚」に2回入らないといけないので、その隣のコインも1回以上、つまり、2回裏返る必要がある。
以下、同様にして、すべての表のコインは2回裏返らないといけないことがわかる。つまり、はじめ表だった5枚のコインは2回裏返すので、表のコインは全部で10回裏返す必要がある。裏のコインは1回か3回裏返すので、全体では、11回か13回裏返すことになる。しかし、どちらの場合も、k=3で割り切れない。よって、すべて表にすることはできない。
解答編 つづき
問題
(3) どのような初期状態であっても必ずこのゲームを終了させることができるための、n、kに関する必要十分条件を求めよ。
解説
「どんな初期状態でもゲームを終了できる」と「1枚だけが裏の状態からゲームを終了できる」が同値であることはすぐに示せます。後者のほうが扱いやすいので、後者で考えていきます。
問2と同じように考えると、表を裏返す回数はすべて同じになることがわかります。また、はじめ裏だったコインも裏返す回数の候補がわかります。これらを組み合わせると、ユークリッドの互除法で出てくる式に似たものがあらわれるので、答えの予想がついてきます。
解答
(3)
1枚が裏の状態からすべて表にできるとすると、その操作を回転して適用することにより、複数のコインが裏の状態からでも表にできる。つまり、「1枚だけが裏の状態からゲームを終了できる」ための必要十分条件を考えればよい。
問2と同様に、それぞれの「連続するk枚」に「操作」を1回適用するかしないかを考えることで、ゲームを行えばよい。このとき、となりあう2つのコインA・Bについて、連続するk枚のコインに入る回数がAよりBのほうが大きくなるものがあるとすると、「Bを出発してAではない方向にk枚」選んだときしかない。また、このとき、回数の差は最大でも1となる。よって、隣り合う2つのコインの裏返る回数が2回以上離れることはない。
1枚だけが裏の状態を考え、すべて表にできるとする。はじめから表だったあるコインの裏返る回数が $2m$ だったとする(mは0以上の整数)と、隣のコインの裏返る回数は2回以上離れないので、表だったコインの裏返る回数はどれも $2m$ 回となる。また、はじめ裏だったコインが裏返る回数は、 $2m-1$ 回か $2m+1$ 回となる。
よって、コインを裏返す回数は全体で、\[2m-1+2m\times (n-1)= 2nm-1\]か、\[2m+1+2m\times (n-1)= 2nm+1\]となる
すべて表になるとき、あるmに対してこれがkで割り切れないといけないので、「kと $2n$ が互いに素」であることが必要。
逆に、「kと $2n$ が互いに素」の場合、 $k,2k,\cdots ,(2n-1)k$ をそれぞれ $2n$ で割った余りはすべて異なる。余りは $1$ 以上 $2n-1$ 以下の整数なので、「 $ak$ を $2n$ で割った余りが $1$ 」となる自然数aが存在する。
裏のコインから時計回りに、$1$ 番目からk番目、$k+1$ 番目から $2k$ 番目、と操作を適用していく。このようにしてa回操作を行うと、裏のコインからはじめて、順番に $ak$ 枚のコインを裏返すことになる( $ak$ 枚目は、はじめ裏だったコイン)。このとき、$ak$をnで割ったときの商は偶数で余りは1なので、すべて表になる。
以上より、求める条件は、「kと $2n$ が互いに素」となる。
解説
個人的にはあまり数式を使いたくないので、上のように解きました。n種類の操作の回数を用いて、各コインの裏返る回数を「mod 2」で考える、というのがよくやるやり方だと思いますが、結構数式はハードになります。「連続するk枚」への操作は高々1回でいいので、わざわざ「mod 2」の世界で考える必要はないかな、と思います。





