センター試験 数学II・数学B 2016年度追試 第1問 [2] 解説
問題編
問題
座標平面上に原点 O を中心とする半径 $2$ の円 C と点 $\mathrm{ A }(4,3)$ がある。
(1) 点 P が C 上を動くとき、線分 AP を $2:1$ に内分する点 Q の軌跡を求めよう。
円 C の方程式は\[ x^2+y^2=\myBox{セ} \quad \cdots ⑤ \]である。 P の座標を $(s,t)$, Q の座標を $(x,y)$ とすると、 Q は AP を $2:1$ に内分するので\[ x=\frac{\myBox{ソ}+\myBox{タ}s}{\myBox{チ}}, y=\frac{\myBox{ツ}+\mybox{タ}t}{\mybox{チ}} \]が成り立つ。よって、 x, y は\[ \left( x-\frac{\myBox{テ}}{\myBox{ト}} \right)^2 +(y-\myBox{ナ})^2 = \left( \frac{\myBox{ニ}}{\myBox{ヌ}} \right)^2 \quad \cdots ⑥ \]を満たし、点 Q の軌跡は $\displaystyle \left( \frac{\mybox{テ}}{\mybox{ト}}, \mybox{ナ} \right)$ を中心とする半径 $\displaystyle \frac{\mybox{ニ}}{\mybox{ヌ}}$ の円である。この円を $C'$ とする。
(2) 円 $C$ と円 $C'$ の二つの交点と原点 O を頂点とする三角形の面積 S を求めよう。
$C$ と $C'$ の二つの交点を通る直線を $\ell$ とする。 $C$ と $C'$ の交点の座標 $(x,y)$ は、等式⑤と⑥を満たす。これらの差をとることにより得られる等式は\[ \myBox{ネ}x+\myBox{ノ}y=15 \]であり、これが $\ell$ の方程式である。また、 O と $\ell$ の距離は $\displaystyle \frac{\myBox{ハ}}{\myBox{ヒ}}$ である。
したがって、 $\displaystyle S=\frac{\myBox{フ}\sqrt{\myBox{ヘ}} }{\myBox{ホ}}$ である。
考え方
軌跡は苦手な人が多いですが、この問題は誘導が丁寧なので、それほど難しくはないでしょう。円 $C'$ の方程式を間違うと残りも間違ってしまうので、慎重に計算しましょう。もし時間があれば、 P を特徴的な点(例えば $(2,0)$ など)として、チェックするのもいいでしょう。また、図形から、円 $C'$ の中心は OA 上に来ることもわかるので、このことをチェックしてもいいです。
最後の三角形の面積は、直角三角形を作ってから考えましょう。交点の座標を求める必要はありません。
解答編
問題
座標平面上に原点 O を中心とする半径 $2$ の円 C と点 $\mathrm{ A }(4,3)$ がある。
(1) 点 P が C 上を動くとき、線分 AP を $2:1$ に内分する点 Q の軌跡を求めよう。
円 C の方程式は\[ x^2+y^2=\myBox{セ} \quad \cdots ⑤ \]である。 P の座標を $(s,t)$, Q の座標を $(x,y)$ とすると、 Q は AP を $2:1$ に内分するので\[ x=\frac{\myBox{ソ}+\myBox{タ}s}{\myBox{チ}}, y=\frac{\myBox{ツ}+\mybox{タ}t}{\mybox{チ}} \]が成り立つ。よって、 x, y は\[ \left( x-\frac{\myBox{テ}}{\myBox{ト}} \right)^2 +(y-\myBox{ナ})^2 = \left( \frac{\myBox{ニ}}{\myBox{ヌ}} \right)^2 \quad \cdots ⑥ \]を満たし、点 Q の軌跡は $\displaystyle \left( \frac{\mybox{テ}}{\mybox{ト}}, \mybox{ナ} \right)$ を中心とする半径 $\displaystyle \frac{\mybox{ニ}}{\mybox{ヌ}}$ の円である。この円を $C'$ とする。
解説

円 C は原点を中心とする半径 $2$ の円なので、この方程式は\[ x^2+y^2=2^2=4 \]となります。
また、 Q は AP を $2:1$ に内分するので、
\begin{eqnarray}
x
&=&
\frac{1\times 4+2\times s}{3} \\[5pt]
&=&
\frac{4+2s}{3} \\[5pt]
\end{eqnarray}と
\begin{eqnarray}
y
&=&
\frac{1\times 3+2\times t}{3} \\[5pt]
&=&
\frac{3+2t}{3} \\[5pt]
\end{eqnarray}が得られます。
$(s,t)$ は C 上の点なので、 $s^2+t^2=4$ が成り立ちます。上で求めた式から
\begin{eqnarray}
3x &=& 4+2s \\[5pt]
s&=&\frac{3x-4}{2}
\end{eqnarray}と
\begin{eqnarray}
3y &=& 3+2t \\[5pt]
t &=& \frac{3y-3}{2} \\[5pt]
\end{eqnarray}となるので
\begin{eqnarray}
\left(\frac{3x-4}{2}\right)^2 +\left(\frac{3y-3}{2}\right)^2 &=& 4 \\[5pt]
\left(x-\frac{4}{3}\right)^2 +(y-1)^2 &=& 4\times \left(\frac{2}{3}\right)^2 \\[5pt]
\left(x-\frac{4}{3}\right)^2 +(y-1)^2 &=& \left(\frac{4}{3}\right)^2 \\[5pt]
\end{eqnarray}が点 Q の軌跡の方程式となります。
解答
セ:4ソタチツ:4233
テトナニヌ:43143
解答編 つづき
問題
(2) 円 $C$ と円 $C'$ の二つの交点と原点 O を頂点とする三角形の面積 S を求めよう。
$C$ と $C'$ の二つの交点を通る直線を $\ell$ とする。 $C$ と $C'$ の交点の座標 $(x,y)$ は、等式⑤と⑥を満たす。これらの差をとることにより得られる等式は\[ \myBox{ネ}x+\myBox{ノ}y=15 \]であり、これが $\ell$ の方程式である。また、 O と $\ell$ の距離は $\displaystyle \frac{\myBox{ハ}}{\myBox{ヒ}}$ である。
したがって、 $\displaystyle S=\frac{\myBox{フ}\sqrt{\myBox{ヘ}} }{\myBox{ホ}}$ である。
解説
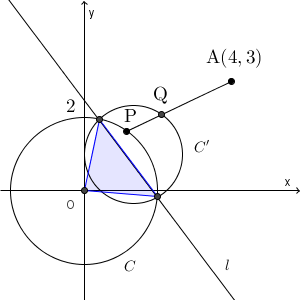
⑤が\[ x^2+y^2=4 \]であり、⑥が\[ \left(x-\frac{4}{3}\right)^2 +(y-1)^2 = \left(\frac{4}{3}\right)^2 \]なので、⑥から⑤を辺々引くと
\begin{eqnarray}
-\frac{8}{3}x+\frac{16}{9}-2y+1 &=& \frac{16}{9}-4 \\[5pt]
-24x+16-18y+9 &=& 16-36 \\[5pt]
-24x-18y &=& -45 \\[5pt]
8x+6y &=& 15 \\[5pt]
\end{eqnarray}となり、これが直線 l の方程式となります。
点と直線の距離の公式から、点 O と直線 l との距離は
\begin{eqnarray}
\frac{|-15|}{\sqrt{8^2+6^2} }=\frac{15}{10}=\frac{3}{2}
\end{eqnarray}となります。
点 O から直線 l に下した垂線をおろすと、斜辺が $2$ で1辺が $\displaystyle \frac{3}{2}$ の直角三角形ができるので、残りの辺の長さは
\begin{eqnarray}
\sqrt{2^2-\left(\frac{3}{2}\right)^2}=\sqrt{\frac{7}{4} }=\frac{\sqrt{7} }{2}
\end{eqnarray}となります。
よって、三角形の面積 S は
\begin{eqnarray}
S
&=&
\frac{1}{2} \times \left(2\times\frac{\sqrt{7} }{2}\right)\times \frac{3}{2} \\[5pt]
&=&
\frac{3\sqrt{7} }{4} \\[5pt]
\end{eqnarray}と求められます。
解答
ネノ:86
ハヒ:32
フヘホ:374





