【基本】命題と集合
ここでは、命題と集合の対応について見ていきます。命題の真偽が、集合の包含関係と対応していることを見ていきます。
例題1
例えば、数人に次のような質問をしたとします。
- 東京ディズニーランド(以下、ランド)に行ったことがあるか
- 東京ディズニーシー(以下、シー)に行ったことがあるか
aさん、bさん、cさん、dさん、eさんの回答が、次のような結果だったとします。○が「行ったことがある」という意味です。
| ランド | シー | |
|---|---|---|
| a | ○ | ○ |
| b | ○ | ○ |
| c | ○ | × |
| d | ○ | × |
| e | × | × |
ここで、次の問題を考えてみます。
(1) ランドに行ったことがある人は、シーにも行ったことがある
(2) シーに行ったことがある人は、ランドにも行ったことがある
まずは、(1)を考えてみます。ランドに行ったことがある人は、a~dの4人ですが、cさんやdさんはシーには行ったことがありません。なので、(1)の文章が常に成り立つわけではないので、「正しくありません」。
次に、(2)ですが、シーに行ったことがある人は、a・bの2人です。この2人はランドにも行ったことがあるので、(2)の文章は「正しい」ことがわかります。
これらのことを数学っぽく言えば、「(1)の命題は偽、(2)の命題は真」となります。(参考:【基本】命題)
また、(1)をもう少し命題っぽく言えば、「xさんがランドに行ったことがあるならば、xさんはシーに行ったことがある」となります。「xさん」には、aさん~eさんの誰かが入ります。「xさんがランドに行ったことがある」が仮定、「xさんはシーに行ったことがある」が結論、となります。
(1)の反例は「xさんがcさんのとき」「xさんがdさんのとき」です。なお、反例をあげるときは、どれか1つだけでかまいません。
これらの用語は、【基本】命題のところで見た内容です。
命題と集合の関係
ここまで、命題の真偽を考えてきました。そのとき、条件を満たす人を考えました。例えば、「シーに行ったことがある人は、ランドにも行ったことがある」という条件を考えたときには、「シーに行ったことがある」という条件を満たす人を具体的に考えました。
このように、命題の真偽を考えるときに、条件を満たす集合と対応させると、考えやすくなります。ベン図を使うと、冒頭の例は次のようになります。

今考えている例では、「シーだけ」という人がいないので、上のような図になります。
この図から、「ランドに行ったことがある人は、シーにも行ったことがある」は間違いであることがわかります。cさんやdさんが入っていないからです。一方、「シーに行ったことがある人は、ランドにも行ったことがある」が正しいことがわかります。シーに行ったことがある人は、ランドに行ったことがある人の集合に属しているからです。
このことを数学っぽく言ってみましょう。
- 条件 p:xさんはランドに行ったことがある
- 条件 q:xさんはシーに行ったことがある
とするとき、上の例題の(1)(2)の解答は次のようになります。
- 命題: $p\implies q$ は偽
- 命題: $q\implies p$ は真
また、条件 p, q を満たす集合を、それぞれ P, Q とすると、ベン図から次が成り立つことがわかります。
- $P \not \subset Q$
- $Q \subset P$

「命題が偽」と「集合が含まれない」、「命題が真」と「集合が含まれる」が、それぞれ対応していることが分かります。
このことを一般的な事柄としてまとめると、次のようになります。
- $p\implies q$ が真であること と $P \subset Q$ となることは同じ
- $p\implies q$ が偽であること と $P \not \subset Q$ となることは同じ
このことは、今考えているランドとシーの例に限らず、数学全般で成り立ちます。これは、「命題の真偽を考えるときは、対応する集合が含まれるかどうかを考えればいい」ということを表しています。
例題2
最後に、もう少し数学っぽい内容を考えて終わりにしましょう。
(1) $|x|\lt 1$ ならば $x \lt 1$
(2) $x\lt 1$ ならば $|x| \lt 1$
数の範囲なので、ベン図ではなく数直線で考えたほうがわかりやすいでしょう。
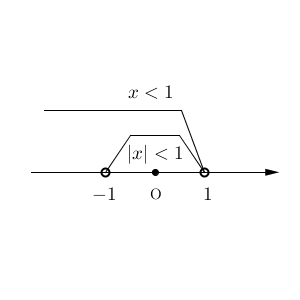
数直線が正しくかければ、 $|x|\lt 1$ を満たす集合が $x \lt 1$ を満たす集合に含まれ、その逆が成り立たないことが分かります。よって、(1)は真、(2)は偽となります。(2)の反例は、例えば $x=-2$ などです。
おわりに
ここでは、命題の真偽と、条件を満たす集合の包含関係が対応していることを見ました。ここで見てきたことは、証明問題を解く上で基礎的な事柄として使われます。ただ、あまりにも基本的なので、参考書や問題集などではわざわざ説明されないことも多いです。





