【基本】正負の数の減法と加法の関係

ここでは、正負の数の減法について振り返った後、加法との関係を見ていきます。

正の数や負の数の減法の復習

【基本】正負の数の減法で見た、正の数や負の数の減法（引き算）について振り返っておきましょう。

$(-2)-(+3)$ のような計算では、「どんな数に $+3$ を足せば、 $-2$ になるか」を数直線で考えたのでした。

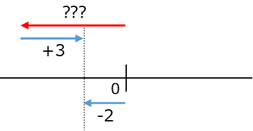
赤い矢印は、「左へ $5$ 移動」に対応するので、 $(-2)-(+3)=-5$ だと計算するのでした。

また、負の数を引く場合も、数直線で考えました。 $(+2)-(-3)$ であれば、「どんな数に $-3$ を足せば、 $+2$ になるか」を考えて

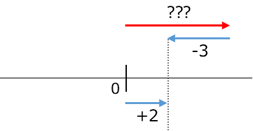
という図から、 $(+2)-(-3)=5$ と計算しました。

ただ、毎回、数直線をかいて考えるのは大変ですね。以下では、数直線をかかずに計算する方法を見ていきます。

正負の数の減法と加法の関係

$(-2)-(+3)$ では、次の「？？？」の部分に入る数字を考えたのでしたね。

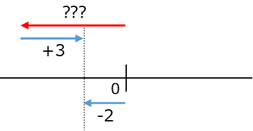
この「？？？」は、 $-2$ から、さらに左に $3$ だけ移動すれば求められます。

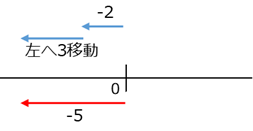
左に $3$ 移動するというのは、 $(-3)$ を足すことに対応しています。つまり、 $(+3)$ を引くことは、 $(-3)$ を足すことと同じなんですね。

これは、例えば、「3万円利益が減る」ことと「3万円損失が増える」ことを考えればわかりやすいでしょう。

一方、 $(+2)-(-3)$ では、次の「？？？」の部分に入る数字を考えたのでした。

この「？？？」は、 $+2$ から、さらに右に $3$ だけ移動すれば求められます。

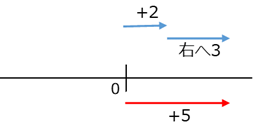
右に $3$ 移動するというのは、 $(+3)$ を足すことに対応しています。つまり、 $(-3)$ を引くことは、 $(+3)$ を足すことと同じなんですね。

これは、先ほどと同じような例を使えば、「3万円損失が減る」ことと「3万円利益が増える」ことを考えればわかりやすいでしょう。

この2つのことをまとめると、「正の数を引く」ことと「負の数を足す」ことは同じで、「負の数を引く」ことと「正の数を足す」ことが同じ、ということです。別の数字での計算例で見てみましょう。
$$\begin{aligned} (+3)-(+5) &= (+3)+(-5) =-2 \\[5pt] (+3)-(-5) &= (+3)+(+5) =8 \end{aligned}$$

このようになります。負の数を引くことが正の数を足すことと同じ、というのは、少しわかりにくいですが、数直線で考えたり、「損失が減る」と考えたり、【導入】気温と負の数の引き算で見た内容を使って、納得しやすいもので考えるようにしましょう。

以上のことをまとめると、次のようになります。

少し変な感じですが、引き算はすべて足し算で置き換えることができます。足し算は、【基本】正負の数の加法で見たように、

　・同符号なら、絶対値の和に、共通の符号をつける。

　・異符号なら、絶対値の大きい方から小さい方を引いて、絶対値が大きい方の符号をつける。

と計算すればいいので、数直線を使わなくても計算できますね。

例題

(1) $(-2)-(+5)$ は、正の数を引くことは負の数を足すことと同じだったので、次のように計算します。
$$\begin{aligned} & (-2)-(+5) \\[5pt] =& (-2)+(-5) \\[5pt] =& -7 \end{aligned}$$

(2) $(-3)-(-1)$ は、負の数を引くことは正の数を足すことと同じだったので、次のように計算します。
$$\begin{aligned} & (-3)-(-1) \\[5pt] =& (-3)+(+1) \\[5pt] =& -2 \end{aligned}$$

(3) $0-(+2)$ は、正の数を引くことは負の数を足すことと同じだったので、次のように計算します。
$$\begin{aligned} & 0-(+2) \\[5pt] =& 0+(-2) \\[5pt] =& -2 \end{aligned}$$

(4) $0-(-2)$ は、負の数を引くことは正の数を足すことと同じだったので、次のように計算します。
$$\begin{aligned} & 0-(-2) \\[5pt] =& 0+(+2) \\[5pt] =& 2 \end{aligned}$$このようになります。

(3)(4)の計算についてよく見てみましょう。どちらも、 $0$ から何かを引く計算ですね。 $+2$ を引くときは、 $-2$ を足すことになるので、答えは $-2$ となります。 $-2$ を引くときは、 $+2$ を足すことになるので、答えは $2$ となります。どちらも、引く数の符号を変えた数字が答えになっていますね。

$0$ から何かを引いたとき、答えは、引く数の符号を変えた数字になります。逆に、何かから $0$ を引いても何も変わりません。

おわりに

ここでは、正の数・負の数の引き算が、足し算で置き換えられる、という話を見てきました。正の数・負の数を引くことは、その数の符号を変えて足すことと同じになります。これで、数直線を使わなくても、引き算をすることができますね。