【基本】文字を使った式で表そう（円周率を使う場合）

ここでは、円周率を用いて、文字を使った式で表す方法を見ていきます。 $\pi$ の紹介も行います。

円周率を表す文字

小学校の算数では、円周や円の面積を求める方法を学びました。このときに、円周率を用いて計算しました。

円周率というのは、円周の直径に対する比 のことです。式で書けば、「円周÷直径」のことで、この値は円の大きさに関わらず一定になります。値は割り切れることはなく、次のように限りなく続く数です。$$3.14159265358979 \cdots$$算数では、円周率を 3.14 として計算するのが普通でした。

中学校では、円周率も文字で表します。 $\pi$ という文字を使います。この $\pi$ というのは、ギリシャ文字の1つで、「パイ」と読みます。この $\pi$ で円周率のことを表します。

例えば、直径 $10$ cmの円の周の長さを求めようと思ったら、$$10\times\pi=10\pi$$と計算し、 $10\pi$ cmと答えます。 $\pi$ は文字の計算と同じように、数字の後に書きます。直径 $1$ cmの円の周の長さであれば、 $1\pi$ cmとは書かず、 $\pi$ cmと書きます。 $1$ を省略するのは、文字のときと同じルールです。

円周率と他の文字との積

円周率 $\pi$ と他の文字とを掛けている場合に、掛け算を省略したときは、円周率のほうを先に書きます。

例えば、半径が $r$ cmの円について考えてみましょう。この円の直径は、2倍すればいいので、 $2r$ cmとなります。これに円周率を掛ければ、円周の長さになりますね。このとき、 $\pi$ は、数字の後、他の文字の前に書きます。つまり、$$2r\times \pi=2\pi r$$と計算し、 $2\pi r$ cmと答えます。

$\pi$ は、1つの決まったある数をあらわす文字なので、他の文字よりも特別扱いします。

円の面積は、半径×半径×円周率で求められるのでした。そのため、半径 $r$ cmの円の面積は、$$r\times r\times \pi = \pi r^2$$という式で求め、 $\pi r^2\ \mathrm{cm}^2$ という答えになります。

算数では、「円周率を3.14とする」と問題文に書かれていることがありましたが、中学では、何も書かれていなければ、 $\pi$ を使って計算します。

例題

(1)は、直径に円周率を掛ければいいですね。$$4\times 2\times \pi=8\pi$$なので、 $8\pi\ \mathrm{cm}$ となります。

(2)は、半径×半径×円周率、で求められます。$$4\times 4\times \pi = 16\pi$$なので、 $16\pi\ \mathrm{cm}^2$ となります。

(3)は、面積は半分になります。なので、(2)の答えを半分にすればいいですね。$$16\pi\div 2=8\pi$$なので、 $8\pi\ \mathrm{cm^2}$ となります。

(4)は、(1)の答えの半分、ではありません。半円は次のような形になります。

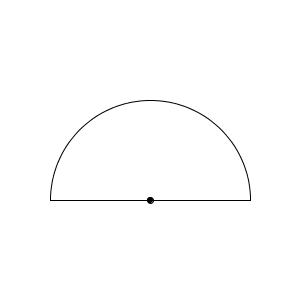
周には、カーブの部分だけでなく、まっすぐの部分も含まれます。そのため、直径も足す必要があります。$$8\pi\div 2+4\times 2=4\pi+8$$と計算できるので、 $(4\pi+8)\ \mathrm{cm}$ が答えとなります。

おわりに

ここでは、円周率を表す文字 $\pi$ を使った式を扱いました。積の中では、数字の後、他の文字の前に置きます。3.14は使わなくなります。 $\pi$ を使った式に慣れていきましょう。