センター試験 数学II・数学B 2018年度追試 第4問 解説
【選択問題】(第3問~第5問から2問選択)
問題編
問題
点O を原点とする座標空間に4点 $\mathrm{ A }(6,-1,1)$, $\mathrm{ B }(1,6,2)$, $\mathrm{ P }(2,-1,-1)$, $\mathrm{ Q }(0,1,-1)$ がある。3点 O, P, Q を通る平面を $\alpha$ とし、 $\overrightarrow{ \mathrm{ OP } }=\vec{p}$, $\overrightarrow{ \mathrm{ OQ } }=\vec{q}$ とおく。平面 $\alpha$ 上に点 M をとり、 $|\overrightarrow{ \mathrm{ AM } }|+|\overrightarrow{ \mathrm{ MB } }|$ が最小となるときの点 M の座標を求めよう。
(1) $|\vec{p}|=\sqrt{\myBox{ア} }$, $|\vec{q}|=\sqrt{\myBox{イ} }$ である。また、 $\vec{p}$ と $\vec{q}$ のなす角は $\myBox{ウエ}^{\circ}$ である。
(2) $\vec{p}$ および $\vec{q}$ と垂直であるベクトルの一つとして\[ \vec{n}=\left(1, \myBox{オ}, \myBox{カ}\right) \]をとる。
$\overrightarrow{ \mathrm{ OA } }$ を実数 $r,s,t$ を用いて $\overrightarrow{ \mathrm{ OA } }=r\vec{n}+s\vec{p}+t\vec{q}$ の形にしたときの $r,s,t$ を求めよう。
$\overrightarrow{ \mathrm{ OA } }\cdot\vec{n}=\myBox{キ}$, $\vec{n} \cdot \vec{n}=\myBox{ク}$, $\vec{n}\perp\vec{p}$, $\vec{n}\perp\vec{q}$ であることから、 $r=\myBox{ケ}$ となる。また、 $\overrightarrow{ \mathrm{ OA } }\cdot\vec{p}$, $\overrightarrow{ \mathrm{ OA } }\cdot\vec{q}$ を考えることにより、 $s=\myBox{コ}$, $t=\myBox{サシ}$ であることがわかる。
同様に、 $\overrightarrow{ \mathrm{ OB } }$ を実数 $u,v,w$ を用いて $\overrightarrow{ \mathrm{ OB } }=u\vec{n}+v\vec{p}+w\vec{q}$ の形に表したとき、 $u=\myBox{ス}$ である。
(3) $r,s,t$ を(2)で求めた値であるとし、点 C は $\overrightarrow{ \mathrm{ OC } }=-r\vec{n}+s\vec{p}+t\vec{q}$ となる点とする。 C の座標は\[ \left( \myBox{セ}, \myBox{ソタ}, \myBox{チツ} \right) \]である。また、線分 BC と平面 $\alpha$ との交点は、 BC を $3:\myBox{テ}$ に内分する。
$\vec{n}\perp\vec{p}$, $\vec{n}\perp\vec{q}$, $\overrightarrow{ \mathrm{ OA } }=r\vec{n}+s\vec{p}+t\vec{q}$, $\overrightarrow{ \mathrm{ OC } }=-r\vec{n}+s\vec{p}+t\vec{q}$ であることにより、線分 AC は平面 $\alpha$ に垂直であり、その中点は $\alpha$ 上にある。よって、 $\alpha$ 上の点 M について、 $|\overrightarrow{ \mathrm{ AM } }|=|\overrightarrow{ \mathrm{ CM } }|$ が成り立ち、 $|\overrightarrow{ \mathrm{ AM } }|+|\overrightarrow{ \mathrm{ MB } }|$ が最小となる M は線分 BC 上にある。したがって、求める M の座標は\[ \left( \dfrac{\myBox{ト} }{\myBox{ナ} }, \dfrac{\myBox{ニヌ} }{\myBox{ネ} }, \myBox{ノハ} \right) \]である。
考え方
一見すると大変そうな感じがしますが、垂直なベクトルがたくさん出てくるので、計算は見た目ほどしんどくありません。内積をいろいろな表現で表して係数を決めていきましょう。
(3)は、テの部分は、ベクトルの理解が深くないと気づきにくいかもしれません。(2)の最後の内容がどう響いてくるのかをよく考えましょう。
(3)の最後は、詳細な説明がありますが、これを読んでパッと意味が分かるには、図形のセンスが必要でしょう。平面上で最短距離を求めるときにはよくやるテクニックですが、空間ではあまりやらないので、なかなかわかりにくいと思います。ただ、意味が分からなくても、問題文をよく読めば、BC と平面 $\alpha$ との交点を考えればいいということはわかりますが。
【選択問題】(第3問~第5問から2問選択)
解答編
問題
点O を原点とする座標空間に4点 $\mathrm{ A }(6,-1,1)$, $\mathrm{ B }(1,6,2)$, $\mathrm{ P }(2,-1,-1)$, $\mathrm{ Q }(0,1,-1)$ がある。3点 O, P, Q を通る平面を $\alpha$ とし、 $\overrightarrow{ \mathrm{ OP } }=\vec{p}$, $\overrightarrow{ \mathrm{ OQ } }=\vec{q}$ とおく。平面 $\alpha$ 上に点 M をとり、 $|\overrightarrow{ \mathrm{ AM } }|+|\overrightarrow{ \mathrm{ MB } }|$ が最小となるときの点 M の座標を求めよう。
(1) $|\vec{p}|=\sqrt{\myBox{ア} }$, $|\vec{q}|=\sqrt{\myBox{イ} }$ である。また、 $\vec{p}$ と $\vec{q}$ のなす角は $\myBox{ウエ}^{\circ}$ である。
解説
\begin{eqnarray} |\vec{p}|^2 &=& 2^2+(-1)^2+(-1)^2 \\[5pt] &=& 6 \end{eqnarray}なので、 $|\vec{p}|=\sqrt{6}$ となります。また、 \begin{eqnarray} |\vec{q}|^2 &=& 0^2+1^2+(-1)^2 \\[5pt] &=& 2 \end{eqnarray}なので、 $|\vec{q}|=\sqrt{2}$ となります。成分を使って $\vec{p}$ と $\vec{q}$ との内積を求めると
\begin{eqnarray}
\vec{p}\cdot\vec{q}
&=&
2\cdot 0
+(-1)\cdot 1
+(-1)\cdot (-1) \\[5pt]
&=&
0-1+1 \\[5pt]
&=&
0
\end{eqnarray}なので、2つのベクトルのなす角は $90^{\circ}$ となります。
解答
ア:6
イ:2
ウエ:90
解答編 つづき
問題
(2) $\vec{p}$ および $\vec{q}$ と垂直であるベクトルの一つとして\[ \vec{n}=\left(1, \myBox{オ}, \myBox{カ}\right) \]をとる。
解説
$\vec{n}=(1,x,y)$ とします。 $\vec{p}$ と $\vec{n}$ の内積は $0$ になるので
\begin{eqnarray}
2\cdot 1+(-1)x+(-1)y &=& 0 \\[5pt]
x+y &=& 2 \\[5pt]
\end{eqnarray}が成り立ちます。また、 $\vec{q}$ と $\vec{n}$ の内積も $0$ になるので
\begin{eqnarray}
0\cdot 1+1\cdot x+(-1)y &=& 0 \\[5pt]
x-y &=& 0 \\[5pt]
\end{eqnarray}が成り立ちます。この連立方程式を解いて、 $x=y=1$ が得られます。よって、\[ \vec{n}=(1,1,1) \]となります。
解答
オカ:11解答編 つづき
問題
$\overrightarrow{ \mathrm{ OA } }$ を実数 $r,s,t$ を用いて $\overrightarrow{ \mathrm{ OA } }=r\vec{n}+s\vec{p}+t\vec{q}$ の形にしたときの $r,s,t$ を求めよう。
$\overrightarrow{ \mathrm{ OA } }\cdot\vec{n}=\myBox{キ}$, $\vec{n} \cdot \vec{n}=\myBox{ク}$, $\vec{n}\perp\vec{p}$, $\vec{n}\perp\vec{q}$ であることから、 $r=\myBox{ケ}$ となる。また、 $\overrightarrow{ \mathrm{ OA } }\cdot\vec{p}$, $\overrightarrow{ \mathrm{ OA } }\cdot\vec{q}$ を考えることにより、 $s=\myBox{コ}$, $t=\myBox{サシ}$ であることがわかる。
解説
成分を用いて内積を求めると、\begin{eqnarray} \overrightarrow{ \mathrm{ OA } }\cdot \vec{n}=(6,-1,1)\cdot(1,1,1)=6-1+1=6 \end{eqnarray}であり、 \begin{eqnarray} \vec{n}\cdot \vec{n}=(1,1,1)\cdot(1,1,1)=1+1+1=3 \end{eqnarray}となります。
また、 $\vec{p}\cdot\vec{n}=0$, $\vec{q}\cdot\vec{n}=0$ なので
\begin{eqnarray}
\overrightarrow{ \mathrm{ OA } }\cdot \vec{n}
&=&
(r\vec{n}+s\vec{p}+t\vec{q})\cdot\vec{n} \\
&=&
r\vec{n}\cdot\vec{n} \\
&=&
3r
\end{eqnarray}となります。 $\overrightarrow{ \mathrm{ OA } }\cdot \vec{n}=6$ だったから、 $r=2$ が得られます。
\begin{eqnarray}
\overrightarrow{ \mathrm{ OA } }\cdot \vec{p}
&=&
(6,-1,1)\cdot (2,-1,-1) \\[5pt]
&=&
12+1-1=12 \\[5pt]
\end{eqnarray}であり、また、 $\vec{n}\cdot\vec{p}=0$, $\vec{q}\cdot\vec{p}=0$ なので
\begin{eqnarray}
\overrightarrow{ \mathrm{ OA } }\cdot \vec{p}
&=&
(r\vec{n}+s\vec{p}+t\vec{q})\cdot\vec{p} \\[5pt]
&=&
s\vec{p}\cdot\vec{p} \\[5pt]
&=&
s|\vec{p}|^2=6s \\[5pt]
\end{eqnarray}となるので、 $s=2$ となります。
\begin{eqnarray}
\overrightarrow{ \mathrm{ OA } }\cdot \vec{q}
&=&
(6,-1,1)\cdot (0,1,-1) \\[5pt]
&=&
0-1-1=-2 \\[5pt]
\end{eqnarray}であり、また、 $\vec{n}\cdot\vec{q}=0$, $\vec{p}\cdot\vec{q}=0$ なので
\begin{eqnarray}
\overrightarrow{ \mathrm{ OA } }\cdot \vec{q}
&=&
(r\vec{n}+s\vec{p}+t\vec{q})\cdot\vec{q} \\[5pt]
&=&
t\vec{q}\cdot\vec{q} \\[5pt]
&=&
t|\vec{q}|^2=2t \\[5pt]
\end{eqnarray}となるので、 $t=-1$ となります。
解答
キ:6ク:3
ケ:2
コ:2
サシ:-1
解答編 つづき
問題
同様に、 $\overrightarrow{ \mathrm{ OB } }$ を実数 $u,v,w$ を用いて $\overrightarrow{ \mathrm{ OB } }=u\vec{n}+v\vec{p}+w\vec{q}$ の形に表したとき、 $u=\myBox{ス}$ である。
解説
$\vec{n}$ の係数だけを求めたいので、 $\overrightarrow{ \mathrm{ OB } }$ と $\vec{n}$ との内積を考えればいいですね。
まず、成分で書くと
\begin{eqnarray}
\overrightarrow{ \mathrm{ OB } }\cdot\vec{n}
&=&
(1,6,2)\cdot(1,1,1) \\[5pt]
&=&
1+6+2=9
\end{eqnarray}となります。また、 $\vec{p}\cdot\vec{n}=0$, $\vec{q}\cdot\vec{n}=0$ なので
\begin{eqnarray}
\overrightarrow{ \mathrm{ OB } }\cdot \vec{n}
&=&
(u\vec{n}+v\vec{p}+w\vec{q})\cdot\vec{n} \\[5pt]
&=&
u\vec{n}\cdot\vec{n} \\[5pt]
&=&
u|\vec{n}|^2=3u \\[5pt]
\end{eqnarray}となるので、 $u=3$ となります。
解答
ス:3
解答編 つづき
問題
(3) $r,s,t$ を(2)で求めた値であるとし、点 C は $\overrightarrow{ \mathrm{ OC } }=-r\vec{n}+s\vec{p}+t\vec{q}$ となる点とする。 C の座標は\[ \left( \myBox{セ}, \myBox{ソタ}, \myBox{チツ} \right) \]である。
解説
$r,s,t$ は、それぞれ、 $2,2,-1$ と求められたので、
\begin{eqnarray}
\overrightarrow{ \mathrm{ OC } }
&=&
-2(1,1,1)+2(2,-1,-1)-(0,1,-1) \\[5pt]
&=&
(-2+4-0,-2-2-1,-2-2+1) \\[5pt]
&=&
(2,-5,-3) \\[5pt]
\end{eqnarray}となります。
解答
セソタチツ:2-5-3解答編 つづき
問題
また、線分 BC と平面 $\alpha$ との交点は、 BC を $3:\myBox{テ}$ に内分する。
解説
BC を $k:(1-k)$ に内分する点を D とおくと、 $\overrightarrow{ \mathrm{ OD } }=(1-k)\overrightarrow{ \mathrm{ OB } }+k\overrightarrow{ \mathrm{ OC } }$ となります。
もし D が平面 $\alpha$ 上にあるとすると、この平面は O, P, Q を通る平面だったので、 $\overrightarrow{ \mathrm{ OD } }$ を $\vec{n},\vec{p},\vec{q}$ を使って表したとき、 $\vec{n}$ の係数は $0$ となります。
$\overrightarrow{ \mathrm{ OB } }$, $\overrightarrow{ \mathrm{ OC } }$ を $\vec{n}, \vec{p}, \vec{q}$ を使って表したとき、 $\vec{n}$ の係数は、それぞれ $u,-r$ 、つまり、 $3,-2$ だったので、
\begin{eqnarray}
3(1-k)-2k &=& 0 \\[5pt]
5k &=& 3 \\[5pt]
k &=& \frac{3}{5} \\[5pt]
\end{eqnarray}となります。よって、線分 BC と平面 $\alpha$ との交点は、 BC を\[ \frac{3}{5}:\left(1-\frac{3}{5}\right)=3:2 \]に内分することがわかります。
解答
テ:2
解答編 つづき
問題
$\vec{n}\perp\vec{p}$, $\vec{n}\perp\vec{q}$, $\overrightarrow{ \mathrm{ OA } }=r\vec{n}+s\vec{p}+t\vec{q}$, $\overrightarrow{ \mathrm{ OC } }=-r\vec{n}+s\vec{p}+t\vec{q}$ であることにより、線分 AC は平面 $\alpha$ に垂直であり、その中点は $\alpha$ 上にある。よって、 $\alpha$ 上の点 M について、 $|\overrightarrow{ \mathrm{ AM } }|=|\overrightarrow{ \mathrm{ CM } }|$ が成り立ち、 $|\overrightarrow{ \mathrm{ AM } }|+|\overrightarrow{ \mathrm{ MB } }|$ が最小となる M は線分 BC 上にある。したがって、求める M の座標は\[ \left( \dfrac{\myBox{ト} }{\myBox{ナ} }, \dfrac{\myBox{ニヌ} }{\myBox{ネ} }, \myBox{ノハ} \right) \]である。
解説
問題文にあることを確かめてみます。
\begin{eqnarray}
\overrightarrow{ \mathrm{ AC } }
&=&
\overrightarrow{ \mathrm{ OC } }-\overrightarrow{ \mathrm{ OA } } \\[5pt]
&=&
-2r\vec{n} \\[5pt]
\end{eqnarray}であり、 $\vec{n}$ は $\vec{p}$ にも $\vec{q}$ にも垂直なので、線分 AC は、平面 $\alpha$ に垂直であることがわかります。
また、中点は $s\vec{p}+t\vec{q}$ で表される点なので、平面 $\alpha$ 上にあることがわかります。
よって、 A, C は平面 $\alpha$ に対して対称な位置にいるので、平面 $\alpha$ 上の点 M に対して $|\overrightarrow{ \mathrm{ AM } }|=|\overrightarrow{ \mathrm{ CM } }|$ が成り立ちます。
なので、 $|\overrightarrow{ \mathrm{ AM } }|+|\overrightarrow{ \mathrm{ MB } }|$ が最小になる場合とは、 $|\overrightarrow{ \mathrm{ CM } }|+|\overrightarrow{ \mathrm{ MB } }|$ が最小になる場合を考えるのと同じで、線分 BC が平面 $\alpha$ に交わるなら、その交点が最小になる点だということがわかります。
これは、例えば、下の図のような状況で考えてみるといいでしょう。下の図は、今考えている問題の設定を反映しているわけではないですが、考え方を理解するには役立つと思います。
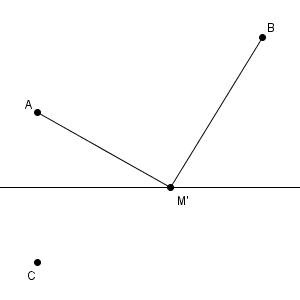
上のような状態で、 AM と BM の長さの和が最小となる場合を考えたいとしましょう。ここで、 M は直線上を動けるとします(上の図では、M' としています)。このとき、この和を直接考えるのは大変ですが、この直線に対して A と対称な位置にある点 C があればどうでしょうか。対称な位置にあるので、 AM と BM の長さの和を考えることは、 CM と BM の長さの和を考えることと同じになります。
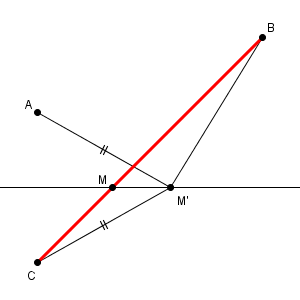
こうなると、長さの和の最小値を見つけることは簡単です。BC を線で結んで、直線と交わる点を考えればいいですね。この問題文では、この考え方を応用すればいい、ということを言っています。つまり、BC と平面$\alpha$ の交点が答えだ、ということです。こうした考えを、3次元の世界で自力で考えろと言われると厳しいですが、誘導があるのでそれにそって考えていけばいいでしょう。
ところで、(3)の前半部分では、線分 BC は、平面 $\alpha$ と交わることを求めていました。なので、この点が答えとなります。その点は、線分 BC を $3:2$ に内分する点だったので
\begin{eqnarray}
\overrightarrow{ \mathrm{ OM } }
&=&
\dfrac{2}{5}(1,6,2)+\dfrac{3}{5}(2,-5,-3) \\[5pt]
&=&
\left(\frac{2+6}{5},\frac{12-15}{5},\frac{4-9}{5}\right) \\[5pt]
&=&
\left(\frac{8}{5},\frac{-3}{5},-1\right) \\[5pt]
\end{eqnarray}となることから、M の座標は\[ \left(\frac{8}{5},\frac{-3}{5},-1\right) \]となります。
解答
トナ:85
ニヌネ:-35
ノハ:-1





