【標準】三角比と正四面体の体積

🕒 2016/11/01 🔄 2023/05/01

ここでは、三角比を用いて正四面体の体積を求めてみます。三角比を使った練習問題です。

📘 目次

三角比と正四面体の体積

次のような、一辺が a の正四面体 ABCD の体積を考えましょう。

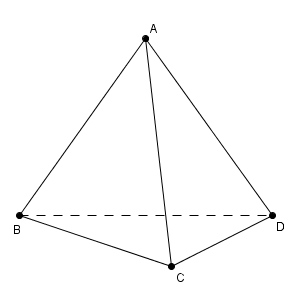
体積を求めるには、底面積と高さがわかればいいですね。底面は正三角形なので、底面積は次のようにして出すことができます。\[ \frac{1}{2}\times a\times\frac{\sqrt{3} }{2}a = \frac{\sqrt{3} }{4}a^2 \]問題は、高さです。

A から底面に垂線をおろし、その足を H とします。この正四面体を、 A, B, H を含む平面で切ります。この平面と CD との交点を M とすると、対称性から M は CD の中点となることがわかります。

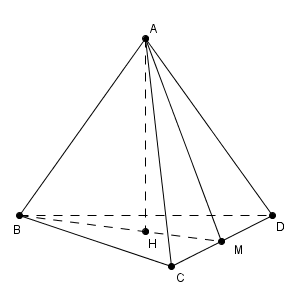
この断面を取り出して考えてみましょう。空間の問題では、このように断面だけを取り出して、平面の問題として考えると解きやすくなることが多いです。 $\mathrm{ AB }=a$ です。また、 M が CD の中点であることから、 $\displaystyle \mathrm{ AM }=\mathrm{ BM }=\frac{\sqrt{3} }{2}a$ であることもわかります。

3辺がわかると、余弦定理が使えます。次のようにして $\cos\angle \mathrm{ ABM }$ が求められます。
\begin{eqnarray} \cos\angle \mathrm{ ABM } &=& \frac{ \mathrm{ AB }^2+\mathrm{ BM }^2-\mathrm{ AM }^2 }{2 \mathrm{ AB }\cdot \mathrm{ BM } } \\[5pt] &=& \frac{ a^2 }{2 a\cdot \frac{\sqrt{3}a}{2} } \\[5pt] &=& \frac{ 1 }{ \sqrt{3} } \\[5pt] \end{eqnarray}となります。

このことから、 AH は
\begin{eqnarray} \mathrm{ AH } &=& \mathrm{ AB }\sin\angle \mathrm{ ABM } \\[5pt] &=& a\sqrt{1-\left(\frac{ 1 }{ \sqrt{3} }\right)^2} \\[5pt] &=& \frac{\sqrt{6} }{3}a \\[5pt] \end{eqnarray}となります。

これから、この正四面体の体積は
\begin{eqnarray} \frac{1}{3} \times \frac{\sqrt{3}a^2}{4} \times \frac{\sqrt{6}a}{3} = \frac{\sqrt{2} }{12}a^3 \end{eqnarray}と求めることができます。

高さについて

上の解き方では、正四面体の高さを求めるときに、断面の三角形に対して余弦定理を用いました。この高さは、他にも求め方があります。

$\triangle \mathrm{ ABH }$, $\triangle \mathrm{ ACH }$, $\triangle \mathrm{ ADH }$ は合同なので、 $\mathrm{ BH }=\mathrm{ CH }=\mathrm{ DH }$ だから、 H は $\triangle \mathrm{ BCD }$ の外接円の中心になります。 BH は外接円の半径なので、正弦定理から\[ \mathrm{ BH }=\frac{a}{2\sin 60^{\circ} }=\frac{\sqrt{3} }{3}a \]となります。三平方の定理から、 $\displaystyle \mathrm{ AH }=\frac{\sqrt{6} }{3}a$ と求めることができます。こうして高さが求められます。

さらに、別の出し方もあります。正三角形の場合、外心と重心は一致するので、 H は $\triangle \mathrm{ BCD }$ の重心でもあります。重心の性質から、 $\mathrm{ BM }:\mathrm{ BH }=3:2$ なので、 $\displaystyle \mathrm{ BH }=\frac{\sqrt{3} }{3}a$ であることがわかります。これから、 $\displaystyle \mathrm{ AH }=\frac{\sqrt{6} }{3}a$ を出すこともできます。

三角比の内容を学ぶと、今まで求められなかったような角や長さが求められるようになります。しかし、一方で、図形の性質を使って解く方法が思いつきにくくなりがちです。図形の性質を使った方が、計算量が少なくなる傾向があるので、三角比を使うべきか、図形の性質は使えないか、という視点を持って問題を解くようにしましょう。