【標準】集合の演算に関する性質
【基本】共通部分と和集合や【基本】補集合で、基本的な集合の演算について見てきました。ここでは、これらの性質をいくつか見ていきます。
これを見て何か新しく問題が解けるようになる、というわけではありませんが、「集合」を勉強するにあたり言葉や記号の意味の理解を深めるのに役立つと思います。
共通部分に関する性質
共通部分とは、次のように「どちらの集合にも属している要素の集合」を言うのでしたね。次のベン図で、塗りつぶしている部分が、共通部分 $A\cap B$ にあたります。

上の図で色のついている部分は、A にも B にも含まれていますね。共通部分の各要素はどちらの集合にも属しているため、共通部分は個々の集合に含まれます。つまり、次が成り立ちます。
もし、集合 A と B に共通部分がない場合は、この式は $\varnothing \subset A$ となります。このことからも、集合は空集合を含む、としたほうがいいことがわかります。
少し変わった見た目ですが、次も成り立ちます。
「A と A の両方に含まれているもの」というのは、A そのものです。また、空集合は何もない集合なので、「空集合にも属している要素」というのはありません。だから、空集合との共通部分は空集合になります。
次の性質はその後の図を見ると、意味がよくわかると思います。

内側の円が A、外側の円が B を表しています。A が B に含まれているときは、「両方に含まれている集合」というのは集合 A そのものになるんですね。
ちなみに、逆も成り立ちます。つまり「 $A\cap B=A$ のとき $A\subset B$ 」も成り立ちます。
和集合に関する性質
和集合は、「少なくとも片方の集合に属している要素の集合」を言うのでした。下の図で、塗りつぶしている部分が、和集合 $A\cup B$ にあたります。
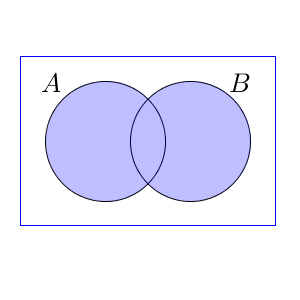
上の図で色のついている部分は、A も B も含んでいます。各集合のすべての要素が和集合に属するため、和集合が個々の集合を含むことは明らかです。つまり、次が成り立ちます。共通部分のときと、包含関係が逆になっているところに注意です。
また、変な例ですが、次も成り立ちます。
包含関係があるときは、次のことが成り立ちます。

A が B に含まれているときは、「どちらかに含まれている集合」というのは集合 B そのものになるんですね。「集合に、その部分集合を足しても、結果は変わらない」ということです。
ちなみに、逆も成り立ちます。つまり「 $A\cup B=B$ のとき $A\subset B$ 」も成り立ちます。
補集合に関する性質
補集合は、「その集合に含まれない要素の集合」を言うのでした。次の図で、塗りつぶしている部分が、補集合 $\overline{ A }$ にあたります。
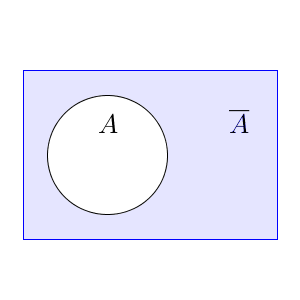
補集合の定義から、「A にも $\overline{ A }$ にも属している要素はない」「どの要素も、A か $\overline{ A }$ に属している」ことがわかります。よって、全体集合を U とおけば、次が成り立ちます。
また、上のベン図を見るとわかると思いますが、「$\overline{ A }$ に属していない要素」の集合は、Aそのものです。よって、次が成り立ちます。
$\overline{U}=\varnothing$ や $\overline{\varnothing}=U$ が成り立つことも、すぐにわかるでしょう。
包含関係があるときは、次のことが成り立ちます。

図を見れば、補集合の包含関係もわかると思います。
おわりに
ここでは、今まで見てきた共通部分や和集合、補集合に関する性質を見てきました。どれも図を描けば納得のいくものばかりだと思います。状況が複雑になってきたら、ベン図を描いて考えましょう。





