【標準】ベクトルの大きさの範囲
ここでは、ベクトルの大きさの範囲を求める問題を考えます。内積を使って解くものを見ていきます。
ベクトルの大きさの範囲
$\vec{a}$, $\vec{b}$ が動くときに、 $|2\vec{a}-\vec{b}|$ がどう動くかはわかりづらいですね。動くものが多すぎて考えづらいです。
$|2\vec{a}-\vec{b}|$ をそのまま扱うのではなく、2乗して考えると扱いやすくなります。2乗をすれば、内積を使って、以下のように考えることができます(参考:【標準】ベクトルの内積と大きさ)。
\begin{eqnarray}
& &
|2\vec{a}-\vec{b}|^2 \\[5pt]
&=&
(2\vec{a}-\vec{b})\cdot(2\vec{a}-\vec{b}) \\[5pt]
&=&
4|\vec{a}|^2-4\vec{a}\cdot\vec{b}+|\vec{b}|^2 \\[5pt]
&=&
4-4\vec{a}\cdot\vec{b}+1 \\[5pt]
&=&
5-4\vec{a}\cdot\vec{b} \\[5pt]
\end{eqnarray}途中で、条件 $|\vec{a}|=1$, $|\vec{b}|=1$ を使っています。
ここまで変形すれば、あとは内積の部分がどういう値かを考えればいいですね。【標準】ベクトルの内積と不等式で見たことから\[ -|\vec{a}||\vec{b}| \leqq \vec{a}\cdot\vec{b} \leqq |\vec{a}||\vec{b}| \]が一般的に成り立ちます。今の場合で言えば\[ -4 \leqq -4\vec{a}\cdot\vec{b} \leqq 4 \]が成り立つということです。このことから、
\begin{eqnarray}
5-4 & \leqq & 5-4\vec{a}\cdot\vec{b} & \leqq & 5+4 \\[5pt]
1 & \leqq & |2\vec{a}-\vec{b}|^2 & \leqq & 9 \\[5pt]
\end{eqnarray}が成り立つことがわかります。 $|2\vec{a}-\vec{b}|$ は0以上なので、\[ 1 \leqq |2\vec{a}-\vec{b}| \leqq 3 \]であることがわかります。
よって、最大値は $3$ で、最小値は $1$ となります。なお、最大となるのは、 $\vec{a}$ と $\vec{b}$ が逆の向き、最小となるのは同じ向きのときです。
この結果から問題をもう一度見直してみると、そりゃあそうか、という気がしますね。 $2\vec{a}$ と $-\vec{b}$ の和の大きさが大きくなるには同じ向きであるほうがよく、小さくなるには反対向きであるほうがいいからです。そして、それぞれのときの大きさは簡単にわかりますね。 $2+1$ と $2-1$ です。
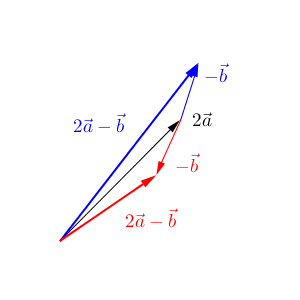
青のように、 $-\vec{b}$ が $2\vec{a}$ と似たような方向だと $2\vec{a}-\vec{b}$ の大きさは大きくなります。一方、赤のように、逆の方向を指すようになると、 $2\vec{a}-\vec{b}$ の大きさは小さくなります。これを突き進めれば、最大になるのは同じ方向、最小になるのは反対の方向のとき、となることがわかりますね。今は、 $\vec{b}$ にマイナスがついているので、少し考えづらいですが。
おわりに
ここでは、ベクトルの大きさの範囲を考える問題を見てきました。そのまま扱うのではなく、2乗して考えることで、内積の性質が利用できるようになります。また、内積の大きさの範囲が角度によって決まることからもわかる通り、ベクトルの和や差の大きさの範囲も、ベクトルのなす角によって決まります。計算によっても、図形によっても考えられるようにしましょう。





