🏠 Home / 数学C / 平面上の曲線 / 二次曲線

【標準】放物線の焦点と準線

🕒 2018/04/14 🔄 2023/05/01

ここでは、放物線の方程式から焦点や準線を求める問題を見ていきます。

📘 目次

放物線の方程式から焦点や準線を求める

【基本】放物線の焦点と準線で見た通り、 $y^2=4px$ のグラフは、点 $(p,0)$ を焦点とし、直線 $x=-p$ を準線とする放物線となります。

これを踏まえて、次のような問題が出題されることが考えられます。

例題

放物線 $y^2=x$ の焦点と準線を求めなさい。

これは、上の式で $p=\dfrac{1}{4}$ としたものですが、焦点・準線と放物線との対応を忘れてしまうこともあるでしょう（係数の4がどこに係ってたか、そもそも係数は4だったか、など）。

そういうときは、ズルいですが、適当な点を使って簡単に計算するようにしましょう。

まず、グラフをかいてみます。原点を通ることはわかりますね。そして、 $(1,\pm1)$ を通ることもわかります。このことから、ざっくりグラフをかくと次のようになります。

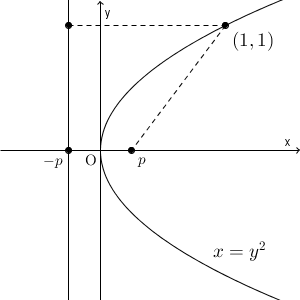
放物線とは、焦点からの距離と準線からの距離が等しい点の軌跡でしたね。焦点を $(p,0)$, 準線を $x=-p$ とおきます。準線と放物線が交わることはないので、 $p\gt 0$ というのもわかりますね。

さて、わかりやすい点として $(1,1)$ があります。この点と準線との距離は $1+p$ ですね。焦点との距離は $\sqrt{(1-p)^2+1^2}$ なので、この2つが等しいとすると
\begin{eqnarray} (1+p)^2 &=& (1-p)^2+1^2 \\[5pt] 4p &=& 1 \\[5pt] p &=& \frac{1}{4} \\[5pt] \end{eqnarray}と求められます。よって、焦点は $\left(\dfrac{1}{4},0\right)$, 準線は $x=-\dfrac{1}{4}$ となることがわかります。

焦点と準線から放物線の方程式を求める

焦点と準線から、放物線の方程式を求める場面（放物線となること自体の説明が不要な場面）もありえます。

例題

焦点が $\left(0,1\right)$, 準線が $y=-1$ となる放物線の方程式を求めなさい。

もしこの問題が「焦点からの距離と準線からの距離が等しい点の軌跡を求めなさい」であれば、軌跡が放物線になることを示す必要があります。しかし、上のような問題文であれば、放物線になること自体は特に問われていなくて、方程式さえ求められればいい、と解釈できます。

このときも、係数の対応を忘れてしまっていると困りますが、これも特別な点を見つけて考えましょう。まずはざっくりとした図をかきます。

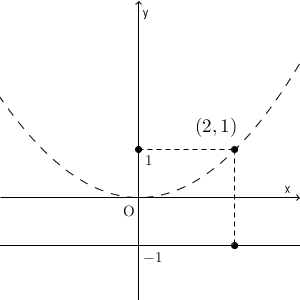
このとき、 $y$ 座標が、焦点と同じ $1$ となる点を考えましょう。この点は準線との距離が $1+1=2$ となることがわかります。ということは、焦点からの距離も $2$ なので、この放物線は $(2,1)$ を通ることがわかります。

放物線の形から $y=ax^2$ の式になることがわかりますが、これに $x=2,y=1$ を入れれば、\[ y=\dfrac{1}{4}x^2 \]となることがわかります。 $x^2=4y$ と答えても構いません。

冒頭に書いた、焦点・準線と放物線の方程式との関係は、教科書に載っている内容であるため、試験などで使っても構いません。ただ、係数は忘れやすいので、上で見たテクニックを使って導けるようにしておけるといいでしょう。このテクニックはこっそりべき使うものなので、答案用紙に書くのはダメですし、軌跡が放物線になることの証明にこれを根拠として使うこともダメです。