【標準】ダブらせて数える

🕒 2017/01/08 🔄 2023/06/13

ここでは、場合の数を求めるときによく使う「ダブらせて数える」方法を見ていきます。

📘 目次

総当たり戦の試合数は何試合か

ここでは、「5つのチームが総当たりのリーグ戦を行うとき、試合数は全部で何試合になるか」という問題を考えてみましょう。「総当たり」とは、「各チームが、他のすべてのチームと試合をする」ということです。

まずは、【基本】書き出して数えるで見たように、すべて書き出してみましょう。

チームを、Ａ，Ｂ，Ｃ，Ｄ，Ｅと書きましょう。まずは、Ａと戦う試合を書き出してみます。すると、対Ｂ，対Ｃ，対Ｄ，対Ｅの4試合あることがわかります。

次に、Ｂと戦う試合を書き出してみます。これも同じように考えると、対Ａ，対Ｃ，対Ｄ，対Ｅになるような気がしますが、「Ｂ対Ａ」という試合は、「Ａ対Ｂ」の試合と同じですね。ダブってしまいます。なので、これを除いた「対Ｃ，対Ｄ，対Ｅ」の3試合があることがわかります。

続いてＣと戦う試合です。対Ａと対Ｂは、Ａ対Ｃ、Ｂ対Ｃがすでに出ているので、ダブってしまいます。なので、「対Ｄ，対Ｅ」の2試合です。

続いてＤです。これは「Ｄ対Ｅ」の試合しかありません。最後はＥですが、Ｅが登場する試合はすでにすべて出てしまっています。

樹形図をかくと、次のようになります。

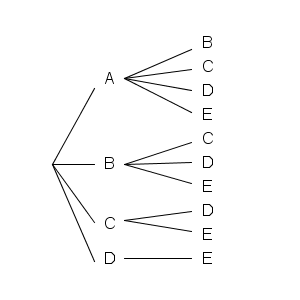
今回は、【基本】まとめて数えるのときと違って、同じ構造が出てきません。なので、掛け算は使えません。総試合数は、それぞれの試合数を足し合わせて\[ 4+3+2+1=10 \]試合と求めることができます。

ダブらせて数えよう

基本的に、数えるときには、ダブらせて数えてはいけません。しかし、自分でコントロールできる場合には、「わざとダブらせて数える」という技が使えることがあります。上で見た「総当たり戦の総試合数」で使うことができます。

Ａと戦う試合は、対Ｂ，対Ｃ，対Ｄ，対Ｅの4試合でした。次にＢと戦う試合を考えたときに、「Ｂ対Ａ」を除きましたね。ダブるからです。しかし、これをあえて残してみます。

Ｃと戦う試合も「Ｃ対Ａ」「Ｃ対Ｂ」を除きましたが残します。Ｄと戦う試合も、Ｅと戦う試合も同様です。Ｅと戦う試合は、4試合除きましたが、すべて残すことにします。

そうなると、「〇対△」という試合は、〇の部分には5チームが入り、△には〇チーム以外の4チームが入ります。なので、今の段階では、\[ 5\times 4=20 \]試合があることがわかります。

ただ、これだとダブっている試合が含まれているので、そのままでは答えになりません。ダブっている試合を除かないといけません。

「あとから除くのなら、はじめから除いておけばよかったのでは？」と思うかもしれませんが、実は、今のケースでは、とてもいいダブり方をしているんですね。

例えば、「Ｂ対Ｅ」という試合。これは「ＢがＥと戦う試合」でもカウントしたし、「ＥがＢと戦う試合」でもカウントしました。１つの試合を2回カウントしています。「Ａ対Ｃ」という試合も「Ａが戦う試合」「Ｃが戦う試合」と、2回カウントします。「〇対△」という試合は、「〇が△と戦う試合」「△が〇と戦う試合」の2回カウントされるんですね。

ということは、どの試合も2重にダブっていることがわかります。なので、2で割れば、求めたい試合数になります。つまり、\[ 5\times 4 \div 2=10 \]試合が求める試合数となります。たしかに、樹形図で求めたときと同じ結果になっています。

総当たりの試合では、次のような表を使うことがあります。

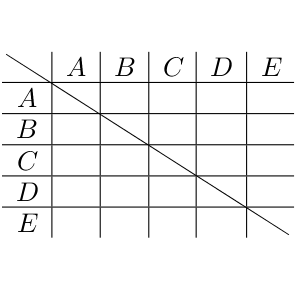
これを見ると、斜線を引いた部分（自分対自分の試合）を除いた試合が $5\times 4=20$ 試合、斜線で折り返したときに重なる部分は同じ試合（Ｂ対ＥとＥ対Ｂなど）なので、すべての試合数は $20\div2=10$ 試合であることがわかります。

もちろん樹形図をかいて解くこともできますが、このようにあえてダブらせることによって簡単に解けることもあります。ここでは5チームでしたが、100チームなら樹形図をかいて解くことは事実上不可能です。しかし、ダブらせて数えるやり方だと、\[100\times99\div2=4950\]試合だ、と簡単に求めることができます。