【標準】和集合の要素の個数
ここでは、和集合の要素の個数を数える問題を見ていきます。【基本】和集合の要素の個数では、2つの集合の和集合を見ましたが、ここでは3つの集合の場合を考えてみます。
3つのどれかで割れるものの個数
2つの集合の場合は、【基本】和集合の要素の個数で考えましたが、そのときと同じようにベン図を使って考えてみましょう。
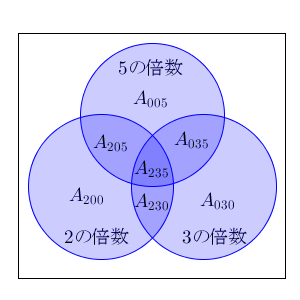
ちょっと変な記号を入れてみました。2だけ、3だけ、5だけで割り切れるものの集合を、それぞれ $A_{200}$, $A_{030}$, $A_{005}$ としています。2と3だけ、3と5だけ、5と2だけで割り切れるものの集合を、それぞれ $A_{230}$, $A_{035}$, $A_{205}$ としています。そして、2と3と5のどれでも割り切れるものの集合を、 $A_{235}$ としています。また、図には出てきていませんが、2の倍数、3の倍数、5の倍数の集合(上の図の円に対応)を、それぞれ $A_2$, $A_3$, $A_5$ と書くことにします。
今求めたいのは、色のついた部分( $A_2\cup A_3\cup A_5$ )に含まれるものの個数です。つまり、上にあげた7つの集合の要素数を合わせたものですね。ただ、これを求めるのに「2の倍数」と「3の倍数」と「5の倍数」を足すだけではだめです。なぜなら、交わっているところをダブって足すことになってしまうからです。( $n(A)$ は集合 A の要素数を表しています)

3つの円をそのまま足すと、2つの円が重なっているところは2回、3つの円が重なっているところは3回足すことになります。少しわかりづらいかもしれませんが、パーツに分けて計算すると以下のようになります。
\begin{eqnarray} & & n(A_2)+n(A_3)+n(A_5) \\[5pt] &=& \{ n(A_{200})+n(A_{230})+n(A_{205})+n(A_{235}) \} \\ & & + \{ n(A_{030})+n(A_{230})+n(A_{035})+n(A_{235}) \} \\ & & + \{ n(A_{005})+n(A_{205})+n(A_{035})+n(A_{235}) \} \\[5pt] &=& \{ n(A_{200})+n(A_{030})+n(A_{005}) \\ & & +n(A_{230})+n(A_{035})+n(A_{205})+n(A_{235}) \} \\ & & + \{ n(A_{230})+n(A_{035})+n(A_{205})+2\times n(A_{235}) \} \\ \end{eqnarray}最後の式の1つ目の波かっこ内だけが求めたいものです。ベン図の中にある細分化された集合が、1回ずつ登場しているのが確認できるはずです。倍数の数をただ足すだけでは、最後の式の2つ目の波かっこが余分に足されてしまうことになります。そこで、【基本】和集合の要素の個数のときと同じように、ダブっているところを引けばいいんじゃないか、という発想が出てきます。2つの集合が重なっている部分は3つあるので、その集合の要素数を足すと、次のようになります。
\begin{eqnarray}
& & n(A_2\cap A_3)+n(A_3\cap A_5)+n(A_5\cap A_2) \\[5pt]
&=&
\{ n(A_{230})+n(A_{235}) \} \\[5pt]
& & + \{ n(A_{035})+n(A_{235}) \} \\[5pt]
& & + \{ n(A_{205})+n(A_{235}) \} \\[5pt]
&=&
\{ n(A_{230})+n(A_{035})+n(A_{205})+ 2\times n(A_{235}) \} \\[5pt]
& & + n(A_{235}) \\[5pt]
\end{eqnarray}ここで、上の式と見比べてみると、 $n(A_{235})$ の部分だけズレがあります。つまり、「2つの集合が重なっている部分」を3か所引くと、今度は「3つの集合が重なっている部分が1回余分に引かれてしまう」ということです。そのため、これを後で足さないといけません。
まとめると、こういうことです。

- 3つの円に含まれる要素数をそのまま足すと、2つの円が重なる箇所を2回、3つの円が重なる箇所を3回数えることになる
- そのため、2つの円が重なる3つの箇所を引く
- その結果、2つの円が重なる箇所を数える回数は1回になるが、3つの円が重なる箇所は数えないことになってしまう
- そのため、3つの円が重なる箇所を足す
\begin{eqnarray} n(A\cup B \cup C) &=& n(A)+n(B)+n(C) \\ & & -n(A \cap B)-n(B\cap C)-n(C\cap A) \\ & & +n(A \cap B \cap C) \\ \end{eqnarray}
これに基づいて例題を解くと、2の倍数は50個、3の倍数が33個、5の倍数が20個で、6の倍数が16個、15の倍数が6個、10の倍数が10個、そして30の倍数が3個なので\[ 50+33+20 -16-6-10 +3 = 74 \]個と求められます。
すごく複雑なことをしているように見えますが、実際に手を動かして計算してみるとたいして難しいことをしているわけではないことがわかるでしょう。ダブっているところを順番に処理していってるだけです。
おわりに
ここでは、3つの集合の和集合の要素の個数を求める問題を見ました。2つの場合と比べ状況が複雑になりましたが、「ダブって数えた後に、不要な部分を引く」という発想と、ベン図を使う点は共通しています。式には規則性があるので、内容が分かればそれほど難しくはないでしょう。





