🏠 Home / 数学II / 図形と方程式 / 直線と方程式

【標準】定点を通る直線

🕒 2017/08/01 🔄 2023/05/01

ここでは、直線をいろいろ動かしたときに、定点を通るようなケースについて見ていきます。

📘 目次

定点を通る直線

例題

k を定数とする。直線\[ (2+k)x+(1-3k)y-5k-3=0 \]は、 k の値によらず、ある定点 A を通る。 A の座標を求めなさい。

k をいろいろ動かしても、定点を通る。うーん、本当でしょうか。実際にやってみましょう。

どうやら、確かにある点を通っているようですね。この座標はどうやって求めればいいでしょうか。

この座標を $(p,q)$ とおけば、このように言い換えることができます。「どんな k に対しても、\[ (2+k)p+(1-3k)q-5k-3=0 \]が成り立つ」と。どんな値を入れてもその点を通るということは、どんな値を入れても等式が成り立つということですからね。こういう「どんな値を入れても成り立つ」という話は、過去に出てきたことがあります。【基本】恒等式のところで見た、恒等式です。

どんな k を入れても成り立つということは、 k についての恒等式になっているということです。そのため、 k について\[ (2p+q-3)+k(p-3q-5)=0 \]と整理します。【基本】恒等式と係数比較で見た内容から、係数比較により
\begin{eqnarray} \left\{ \begin{array}{l} 2p+q-3=0 \\ p-3q-5=0 \end{array} \right.\end{eqnarray}を解けばいいことがわかります。2つ目の式を2倍して1つ目の式から引けば \begin{eqnarray} 7q+7 &=& 0 \\ q &=& -1 \\ \end{eqnarray}が得られ、2つ目の式から \begin{eqnarray} p&=&3q+5 \\ &=&2 \end{eqnarray}が得られます。以上から、定点の座標は $(2,-1)$ となることがわかります。

なお、ここでは、説明のために $(p,q)$ とおきましたが、このように置く必要はありません。 $(x,y)$ のまま書いても構いません。

また、上では係数比較によって求めましたが、【基本】恒等式と数値代入で解くことも一応できます。ただ、「いくつか値を入れて条件式を作って座標を求める ⇒ 他の直線も求めた点を通っているかを調べる」という手順が必要です。後半部分を忘れやすいので注意しましょう。個人的には、係数比較のほうが楽に解けるように思います。

なんの直線の集まりだったのか

上の例題はすでに解けたのですが、出てきた式について少し考えてみましょう。元の式を変形して\[ (2x+y-3)+k(x-3y-5)=0 \]の形にしてから、各カッコ内が $0$ になる点を求めましたね。 k を動かすと、直線の位置はいろいろ変化しますが、必ずこの点を通るのでした。

連立方程式を解いたことからもわかる通り、この点は、2つの直線 $2x+y-3=0$ と $x-3y-5=0$ の上にもあります。

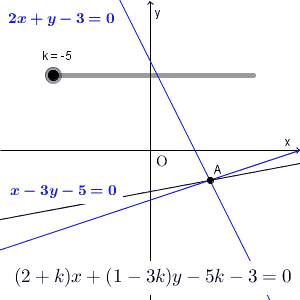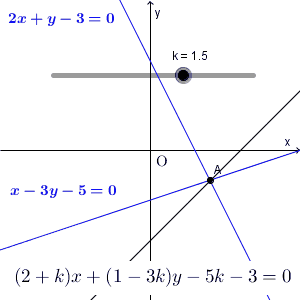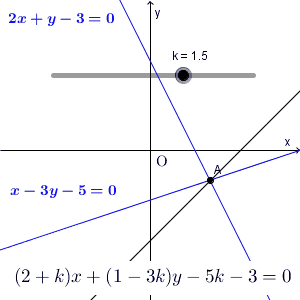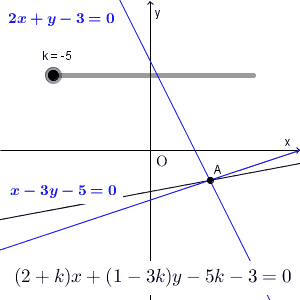
つまり、上の例題で考えた直線は、2つの直線 $2x+y-3=0$ と $x-3y-5=0$ の交点を通る直線が集まったもの、と考えることもできます。

ただ1つ注意が必要なのは、上の例題で出てきた直線は、この2直線の交点を通る直線だけど、すべてを表しているわけではない、という点です。上の動画を見ると、 $k=0$ のときに $2x+y-3=0$ とぴったり重なっていますが、 $x-3y-5=0$ とは重なりません。これは k の動かす範囲が狭いからではなく、どんな値を入れても重なることはないんですね。このあたりの話は、また別の機会に譲ることにします。