【標準】ベクトルの内積と不等式
ここでは、ベクトルの内積がからんだ不等式をいくつか見ていきます。
ベクトルの内積に関する不等式
ここでは、内積の大きさについて考えてみましょう。
$\vec{a}$ と $\vec{b}$ が $\vec{0}$ でないとき、内積 $\vec{a}\cdot\vec{b}$ は、\[ |\vec{a}||\vec{b}|\cos\theta \]と書けるのでしたね。この $\cos$ の値は、 $-1$ から $1$ の値をとります(参考:【基本】よく出る0度から180度までの三角比の値)。そのため、次の不等式が成り立つことがわかります。\[ -|\vec{a}||\vec{b}| \leqq \vec{a}\cdot\vec{b} \leqq |\vec{a}||\vec{b}| \]なお、左側の等号が成り立つのは、 なす角が $180^{\circ}$ のときなので、向きが反対のときです。右側の等号が成り立つのは、向きが同じときですね。
$\vec{a}$, $\vec{b}$ の少なくとも片方が $\vec{0}$ であれば、 $|\vec{a}||\vec{b}|$ も $\vec{a}\cdot\vec{b}$ も $0$ になるため、このときも上の不等式は成り立ちます。
以上から、この不等式は、つねに成り立つことがわかります。
内積の定義と $\cos$ のとる範囲を考えれば、この不等式が成り立つことは理解できるでしょう。
ベクトルの大きさと三角不等式
両辺が0以上なので、両辺を2乗して引いた値を考えます。【標準】絶対値と不等式の証明でも似た式を扱っており、同じような解き方で考えていきます。実数か、ベクトルか、という点が違うので、全く同じわけではありませんが。
さて、右辺を2乗したものから左辺を2乗したものを引くと、次のようになります。
\begin{eqnarray}
& &
(|\vec{a}|+|\vec{b}|)^2-|\vec{a}+\vec{b}|^2 \\[5pt]
&=&
|\vec{a}|^2+2|\vec{a}||\vec{b}|+|\vec{b}|^2 \\
& & -(\vec{a}+\vec{b})\cdot(\vec{a}+\vec{b}) \\[5pt]
&=&
2|\vec{a}||\vec{b}| -2\vec{a}\cdot\vec{b} \\[5pt]
&=&
2(|\vec{a}||\vec{b}| -\vec{a}\cdot\vec{b}) \\[5pt]
\end{eqnarray}ここで、最後の式は、上で見た内積の大きさに関する不等式から、0以上であることがわかります。よって、右辺を2乗したものは左辺を2乗したもの以上であることがわかります。両辺は0以上なので、\[ |\vec{a}+\vec{b}| \leqq |\vec{a}|+|\vec{b}| \]が成り立つことが示せました。
なお、等号が成り立つのは、 $\vec{a}$, $\vec{b}$ の少なくとも一方が $\vec{0}$ のときか、なす角が $0^{\circ}$ のときです。
内積 $\vec{a}\cdot\vec{b}$ は、最大でも $|\vec{a}||\vec{b}|$ というのは、上でも見た通り、定義からすぐにわかります。このことは、ベクトルに関する不等式で使うことがあります。
この不等式 $|\vec{a}+\vec{b}| \leqq |\vec{a}|+|\vec{b}|$ を図形的に考えてみましょう。
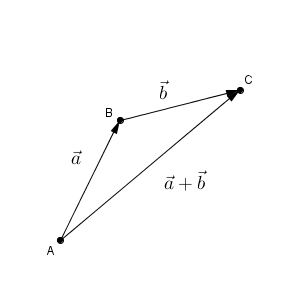
右辺に出てくる $\vec{a}$, $\vec{b}$ と、左辺の $\vec{a}+\vec{b}$ を図にしてみました。右辺が示していることは、A から B を通って C に行くまでの距離です。一方、左辺は A からまっすぐ C に行くときの距離です。図を見れば、右辺が左辺以上になるのは当たり前ですね。まっすぐ行くのが一番の近道ですからね。
この不等式は、三角不等式と呼ばれるものです。一般的に、三角形の一辺の長さは、他の二辺の長さの和を超えることはありません(二頂点間をまっすぐ行くのが一番の近道だからです)。例題の不等式は、これをベクトルで書いているだけです。
また、【標準】絶対値と不等式の証明でも見たように、この例題の不等式から派生した不等式も得られます。\[ |\vec{a}+\vec{b}| \leqq |\vec{a}|+|\vec{b}| \]で、 $\vec{a}$ を $\vec{a}+\vec{b}$ とし、 $\vec{b}$ を $-\vec{b}$ とすると
\begin{eqnarray}
|\vec{a}+\vec{b}-\vec{b}| & \leqq & |\vec{a}+\vec{b}|+|-\vec{b}| \\[5pt]
|\vec{a}|-|\vec{b}| & \leqq & |\vec{a}+\vec{b}| \\[5pt]
\end{eqnarray}が得られます。例題の不等式と合わせて、この不等式も重要です。
おわりに
ここでは、ベクトルの内積に関する不等式を見ました。ベクトルの内積の定義から理解できるものでしたね。ベクトルに関する不等式や、ベクトルに関する最大・最小を求める問題で使うことがあります。





