【標準】双曲線の焦点

🕒 2018/04/16 🔄 2023/05/01

ここでは、双曲線の方程式から焦点の座標を求める問題を見ていきます。

📘 目次

双曲線の方程式から焦点を求める

【基本】双曲線の焦点（焦点がx軸上）で見たように、 $a,b\ne0$ のとき、 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2} = 1$ のグラフは、 $(-\sqrt{a^2+b^2},0)$, $(\sqrt{a^2+b^2},0)$ の2点を焦点とする双曲線となります。これを踏まえて、次のような問題が出題されることがあります。

例題

双曲線 $4x^2-9y^2=36$ の焦点の座標を求めなさい。

冒頭の対応がよくわかるように、右辺が $1$ になるように変形します。\[ \frac{x^2}{9}-\frac{y^2}{4}=1 \]このことから、焦点の座標は $(-\sqrt{13},0)$, $(\sqrt{13},0)$ であることがわかります。

ただ、方程式の係数と焦点の座標の対応を忘れてしまうこともあるでしょう。その場合は、図を利用し、次のようにして思い出すようにしましょう。

まずわかることは、この双曲線が $(3,0)$, $(-3,0)$ を通る、ということですね。また、【基本】双曲線と漸近線で見たように、漸近線を考えましょう。これは、双曲線の方程式の左辺を因数分解したときに出てくる式\[ \left(\dfrac{x}{3}-\dfrac{y}{2}\right)\left(\dfrac{x}{3}+\dfrac{y}{2}\right) \]を利用して、\[ y=\frac{2}{3}x,\ y=-\frac{2}{3}x \]となるのでした。感覚的には、「 $x,y$ が大きいときは、右辺は無視できるほど小さくなる」ことから理解できるでしょう。

これらをもとに、双曲線のグラフをかいてみます。

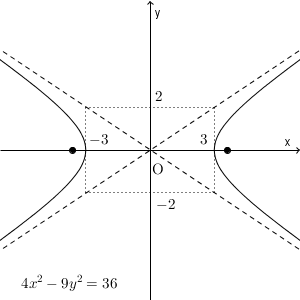
$(3,0)$, $(-3,0)$ を通っていますね。また、2つの直線 $x=3$, $x=-3$ と漸近線との交点は、漸近線の式から、 y 座標が $2,-2$ であることがわかります。この4つの交点をつなぐと、長方形ができます。

ここで、冒頭で見た係数の対応をよく見てみましょう。まず、頂点にあたる点の座標は $(a,0)$, $(-a,0)$ にあたります。また、漸近線の方程式は $\dfrac{x}{a}-\dfrac{y}{b}=0$, $\dfrac{x}{a}+\dfrac{y}{b}=0$ となるため、漸近線と2つの直線 $x=a$, $x=-a$ との交点の y 座標は $b,-b$ であることがわかります。この4つの交点をつなぐと、長方形ができます。

ところで、冒頭で見たように、焦点の座標は $(-\sqrt{a^2+b^2},0)$, $(\sqrt{a^2+b^2},0)$ となります。これは、この長方形の対角線の半分です。これらを踏まえて、次のように円をかいてみます。

漸近線と2つの直線 $x=a$, $x=-a$ との4つの交点（ $(a,b)$, $(a,-b)$, $(-a,b)$, $(-a,-b)$ の4点）、および、焦点は、同じ円周上にあります。このことを視覚的に覚えておけば、焦点の座標が $(-\sqrt{a^2+b^2},0)$, $(\sqrt{a^2+b^2},0)$ であることが思い出せるでしょう。