【標準】点と直線との距離
ここでは、点と直線との距離について考えます。
点と直線との距離
【基本】原点と直線との距離では、原点と直線との距離について考えましたが、ここでは原点ではなく一般の点からの距離について見ていきます。
点 $\mathrm{ P }(p,q)$ と直線 $l:\ ax+by+c=0$ との距離を求めてみましょう。ただ、一から求めるのは面倒です。原点からの距離はすぐに求められるのだから、それを使いまわす方法を考えましょう。
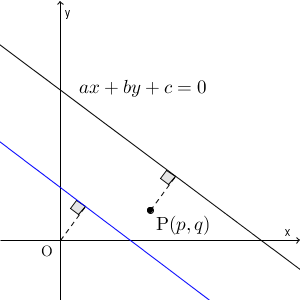
点と直線をセットで平行移動しても、距離は変わりません。よって、点 P が原点にくるように直線を平行移動し、その直線と原点との距離を求めればいいですね。この移動した後の直線(上の図の青い直線)を $l'$ と書くことにしましょう。
直線が y 軸と平行ではない場合、つまり、 $b\ne 0$ の場合、直線 l は\[ y=-\frac{a}{b}x-\frac{c}{b} \]と書けます。 l と $l'$ は平行なので傾きは同じです。
また、直線 l の切片の座標は $\left(0,-\dfrac{c}{b}\right)$ ですが、平行移動をした後に、この点は $\left(-p,-\dfrac{c}{b}-q\right)$ に移動します。 $l'$ はこの点を通ります。
よって、 $l'$ の方程式は
\begin{eqnarray}
y -\left(-\dfrac{c}{b}-q\right) &=& -\frac{a}{b} (x+p) \\[5pt]
by+c+bq &=& -a(x+p) \\[5pt]
ax+by+(ap+bq+c) &=& 0 \\[5pt]
\end{eqnarray}となります。最後のカッコの中全体が定数になります。
このことから、原点と直線 $l'$ との距離は、【基本】原点と直線との距離で見た内容から
\begin{eqnarray}
\frac{|ap+bq+c|}{\sqrt{a^2+b^2} }
\end{eqnarray}が距離となります。よって、点 P と直線 l との距離も、この値になります。
元の直線が y 軸と平行である場合は、元の直線は $x=-\dfrac{c}{a}$ なので、これと $(p,q)$ との距離は
\begin{eqnarray}
\left|p-\left(-\dfrac{c}{a}\right)\right| &=& \frac{|ap+c|}{\sqrt{a^2} }
\end{eqnarray}となり、先ほどの式で $b=0$ とした式になることがわかります。よって、先ほどの式は、元の直線が y 軸と平行である場合も含めて使うことができます。
以上のことをまとめると次のようになります。
分母は、原点との距離のときと同じですね。分子の絶対値の中は、直線の方程式に $x=p$, $y=q$ を代入したものになっています。原点との距離の場合は、分子が $|c|$ となっていましたが、これは $x=0$, $y=0$ を代入したからだ、と考えることができます。
例えば、 $(2,1)$ と $3x+4y+5=0$ との距離は
\begin{eqnarray}
\frac{|3\cdot 2+4\cdot 1+5|}{3^2+4^2} = \frac{15}{5} = 3
\end{eqnarray}となります。式自体は少し複雑に感じますが、実際に使ってみるとかなり簡単に距離を出すことができます。もしこれを知らなければ、垂線をおろしてその直線の方程式を求める、交点の座標を求める、三平方の定理を使う、などの手順を踏む必要があり、計算が大変です。
この式は、座標を使って図形的な問題を解くときによく使われます。
おわりに
ここでは、点と直線との距離について考えました。\[ \frac{|ap+bq+c|}{\sqrt{a^2+b^2} } \]という式はよく出てくるので、しっかり押さえておきましょう。





