🏠 Home / 数学II / 微分と積分の基礎 / 微分と三次関数のグラフ

【標準】三次関数と微分

🕒 2017/10/24 🔄 2023/05/01

ここでは、一般的な三次関数のグラフがどうなるかを、微分を用いて考えていきます。

📘 目次

三次関数と微分

一般的な三次関数 $f(x)=ax^3+bx^2+cx+d$ に対し、グラフ $y=f(x)$ がどうなるかを考えていきます。なお、 $a\gt 0$ の場合を考えます。

x がすごく小さいときは y も小さい値をとり、 x がすごく大きければ y もすごく大きくなります。 $ax^3$ の影響が大きくなるからです。そのため、グラフは左下から最終的には右上に伸びていく形となります。

ただし、間に山や谷があるかもしれません。これらがあるかどうかは、微分をしてその符号を調べる必要があるのでしたね。

微分をした結果は、\[ y'=3ax^2+2bx+c \]となります。この符号がどうなるかを調べていきます。

$a\gt 0$ なので、導関数のグラフは下に凸の放物線となります。なので、取りうる符号のパターンは、「負の値をとることもある」「つねに $0$ 以上」「つねに正」のどれかしかありません。そして、それぞれの場合について、判別式は、正、 $0$ 、負、ときれいに分かれます。（参考：【基本】二次関数のグラフとx軸との共有点）

まず、判別式が正の場合、つまり
\begin{eqnarray} (2b)^2 -4 \cdot 3a \cdot c & \gt & 0 \\[5pt] b^2 -3ac & \gt & 0 \\[5pt] \end{eqnarray}の場合を考えてみましょう。

この場合、導関数のグラフは x 軸と2点で交わります。この2点の x 座標を、小さい方から $\alpha, \beta$ としておきます。

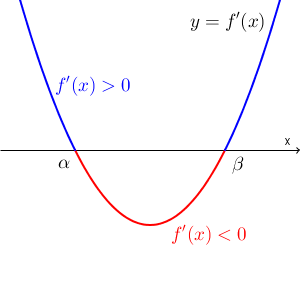
導関数の符号は、正⇒負⇒正、と変化していきます。そのため、このときの増減表は次のようになります。
\begin{array}{c|ccccc} x & \cdots & \alpha & \cdots & \beta & \cdots \\ \hline f’(x) & + & 0 & – & 0 & + \\ \hline f(x) & \nearrow & f(\alpha) & \searrow & f(\beta) & \nearrow \end{array}よって、グラフは、次のように山も谷もあるグラフになります。

このとき、 $y=f(x)$ は、 $x=\alpha$ で極大となり、 $x=\beta$ で極小となる、というのでしたね。また、 $f(\alpha)$ を極大値、 $f(\beta)$ を極小値というのでした（参考：【基本】極大値と極小値）。

さて、次に、判別式が $0$ の場合、つまり、\[ b^2 -3ac = 0 \]のときを考えましょう。このとき、導関数のグラフと x 軸との共有点は1点となります。この点の x 座標を $\alpha$ とします。

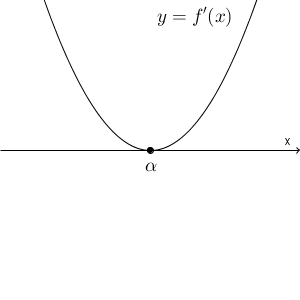
このときの増減表は次のようになります。
\begin{array}{c|ccc} x & \cdots & \alpha & \cdots \\ \hline f’(x) & + & 0 & + \\ \hline f(x) & \nearrow & f(\alpha) & \nearrow \end{array}よって、グラフは、次のように山も谷もないグラフになります。

$x=\alpha$ のまわりで導関数の符号は変わりません。そのため、この点では極値をとる、とはいいません。導関数が $0$ でも、極値をとるとは限りません。

この場合、この関数はずっと増え続けるため、単調増加である、というのでしたね。

最後に、判別式が負の場合、つまり、\[ b^2 -3ac \lt 0 \]のときを考えましょう。このとき、導関数のグラフは x 軸と共有点を持たず、つねに x 軸のうえにあります。

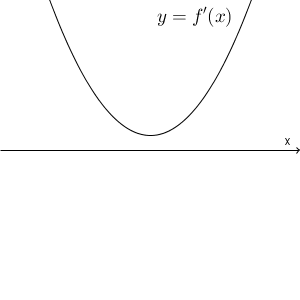
よって、増減表は、次のようになります。
\begin{array}{c|c} x & \cdots \\ \hline f’(x) & + \\ \hline f(x) & \nearrow \end{array}この場合は、増減表を書かずに「導関数はつねに正である」と言葉で済ますこともあります。グラフは次のようになります。

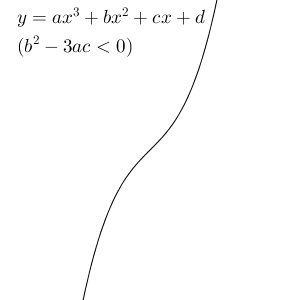
判別式が $0$ の場合とよく似ていますが、微分係数が $0$ になる瞬間があるかどうかが違うだけですね。この場合も、つねに増え続けるので、単調増加です。

三次関数のグラフは、この3つのどれかのパターンになります。大きく分けると、山と谷があるパターンと山も谷もないパターンがあり、後者は、さらに、微分係数が $0$ になるときがあるかないか、で分かれるということですね。なお、 $a\lt 0$ のときは、上下が反転するだけで、同じように考えることができます。