【発展】和の公式（1からnまでの和）と四角形

🕒 2018/02/02 🔄 2023/05/01

ここでは、 $1$ から n までの和や奇数の和の公式について、図形的な観点から理解していきます。入試などには出ませんが、理解は深まると思います。

📘 目次

nまでの和と長方形

下の図のように、1段目には1つ、2段目には2つ、…と、正三角形になるように、上から順番に円を並べていきます。

上から n 段目までに並んでいる円の数が、 $1$ から n までの和となります。 n 段目までの円の数を、この図にちなんで三角数(triangular number) といいます。つまり、 $1$, $3$, $6$, $10$, $15$, $21$, $\cdots$ などを三角数と呼ぶ、ということです。

n 段目までの円の数を求めるために、円の並び方を少し変えてみます。左に揃えるようにしてみましょう。

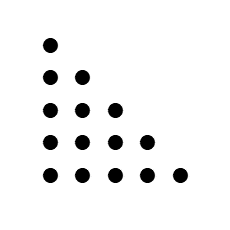
このようにしてから上下さかさまにした三角形を隣に並べれば、長方形が出来上がります。

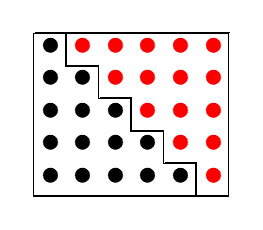
縦には n 個の円があり、横には $n+1$ 個の円があります（上の図は $n=5$ の場合です）。なので、 n 段目までの円の数、言い換えれば、 $1$ から n までの和は\[ \frac{1}{2}n(n+1) \]となることがわかります。

小学生の時に、三角形の面積の出し方を習いますが、そこでも似たことをしました。同じ三角形を2つ使って片方をひっくり返せば四角形を作ることができるので、三角形の面積は「底辺×高さ÷2」で求められるのでしたね。

【基本】和の公式（1からnまでの和）で、 $1$ から n までの和を出すときに、足す順番を逆にしたものを考えましたが、これは三角形の面積を出すときの考え方に共通する部分がありますね。

nまでの和と正方形

先ほど、三角形状に並べた円と、それをひっくり返したものを組み合わせて、長方形を作りました。

横が1列多いので長方形になってしまってますね。これをうまく1列減らして、正方形のようにできないかな、と考えてみましょう。そうすると、次のようにすればうまく収まることがわかります。

n 段の三角形と $(n-1)$ 段の三角形を組み合わせるようにする、ということです。こうすると、正方形になることがわかります。計算でも確かめてみましょう。

n 段の三角形には、 $\dfrac{1}{2}n(n+1)$ 個の円があります。また、右上は $(n-1)$ 段の三角形なので、円の数は\[ \frac{1}{2}(n-1)(n-1+1)=\frac{1}{2}n(n-1) \]となります。 n を $n-1$ に置き換えています。

この2つを足すと
\begin{eqnarray} & & \frac{1}{2}n(n+1)+\frac{1}{2}n(n-1) \\[5pt] &=& \frac{1}{2}n\{(n+1)+(n-1)\} \\[5pt] &=& \frac{1}{2}n\times 2n \\[5pt] &=& n^2 \end{eqnarray}となり、確かに、1辺が n の正方形の面積（正方形に含まれる円の数）となります。

「 $1$ から $n$ までの和と $1$ から $n-1$ までの和を足すと、 $n^2$ になる」。式から思いつくのは難しいですが、図からだと思いつきやすいかもしれません。

ちなみに、先ほど紹介した「三角数」という言葉を使えば、「2つの連続する三角数の和は、平方数になる」ともいえます。

奇数の和と正方形

さて、【基本】和の公式（1からnまでの和）では、奇数の和についても見ました。\[ 1+3+5+\cdots+(2n-1)=n^2 \]この右辺は、ここまで見た内容と照らし合わせると、正方形の面積と見ることもできますね。では、正方形を「奇数の和」と見ることはできるでしょうか。このすぐ後に答えがあるので、考えたい人は以下を見る前に少し考えてみましょう。

奇数の和と正方形については、結論が分かっているので、（ズルいですが）結論から考えてしまいましょう。「 $n$ 番目までの奇数の和が $n^2$ になる」ということから予想してみます。すると、奇数を1つ増やすと、正方形の1辺の長さが1増えることに対応するとわかるため、次のように区切るのがいいのではないか、と考えることができます。

このように分けると、それぞれの┛の部分（逆Ｌ字の部分）に奇数個の円が並ぶことになります。次のように色付けするとさらにわかりやすくなります。

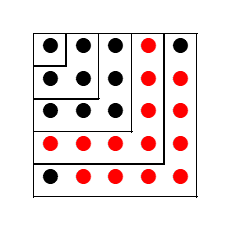
4つ目の逆Ｌ字と5つ目の逆Ｌ字で考えてみます。このとき、4つ目の逆Ｌ字の部分を全体的に右下に移動すれば、5つ目の逆Ｌ字の部分に対応します。ただ、5つ目の逆Ｌ字の部分の、右上の部分と左下の部分の2つの円が対応していません。なので、逆Ｌ字の部分は1つ進むと円が2個増えることがわかります。

1つ目には円が1つ、2つ目には円が3つ、3つ目には円が5つ、というように、 n 番目の逆Ｌ字には円が「n 番目の奇数個」あることがわかります。また、 n 個の逆Ｌ字を全部合わせれば、一辺が n の正方形になります。\[ 1+3+5+\cdots+(2n-1)=n^2 \]となることを、図形的な観点から理解することができます。