【導入】二次曲線

過去に、 $y=ax^2$ という関数のグラフを扱ったことがありますよね。このグラフを、放物線と呼びます。また、 $y=\dfrac{a}{x}$ という関数のグラフも扱ったことがあります。このグラフは、双曲線といいましたね。

この2つは全然違う形をしていますが、どちらも、円すいを切ったときの切り口として現れることが知られています。

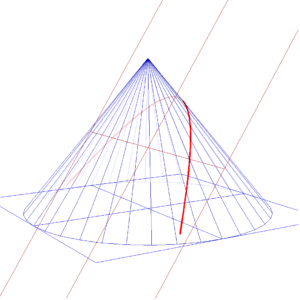
上の図は、円錐の母線と平行な平面で切ったときの図で、このときの断面には放物線が現れます。また、図からは少し見にくいですが、切る平面をさらに立たせていく（円すいの底面とのなす角が大きくなるようにしていく）と、双曲線が現れるようになります。

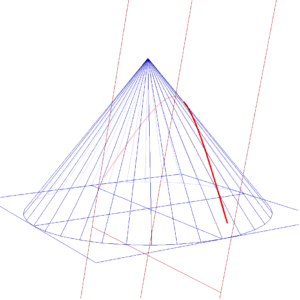
逆に、切る平面を寝かせていく（円すいの底面とのなす角が小さくなるようにしていく）と、次のようになります。

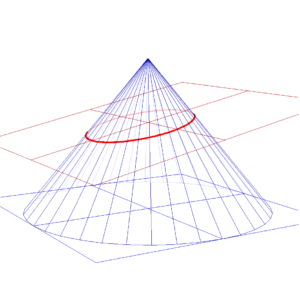
このときの形は、楕円（だえん）といいます。楕円という言葉自体は、日常生活でも耳にしたことがある人もいるかもしれませんね。もちろん、さらに寝かせて、円錐の底面と平行になるときには、切り口は円になります。

これらの放物線、双曲線、楕円、円は、円錐を切ったときに表れる曲線なので、円錐曲線と呼ばれます。また、（今後見ていくことになりますが、）関数で表したときに二次式で表されることから、二次曲線とも呼ばれています。

これから、これらの二次曲線について詳しく見ていくことにします。また、これらの二次曲線はバラバラに見えるかもしれませんが、ここで見た「円錐の切り口」のように、つながりのあるものとして理解する方法についても見ていきます。