【応用】18度の三角比

🕒 2016/09/23 🔄 2023/05/01

ここでは、【応用】36度の三角比で考えた図を用いて、18度の三角比と72度の三角比について見ていきます。

📘 目次

18度の三角比

$\angle \mathrm{ A }=36^{\circ}$ で、 $\mathrm{ AB }=\mathrm{ AC }$, $\mathrm{ BC }=1$ の二等辺三角形 ABC を考えます。点 D は線分 AC 上の点で、 $\angle \mathrm{ BDC }=72^{\circ}$ となる点とします。

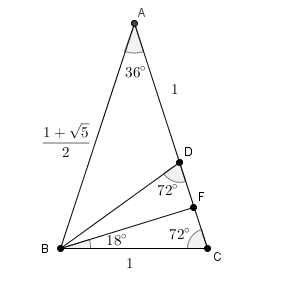
【応用】36度の三角比で見た通り、 $\triangle \mathrm{ ABC }$ と $\triangle \mathrm{ BCD }$ が相似であることから、\[ \mathrm{ AB } =\frac{1+\sqrt{5} }{2} \]であることがわかります。

ここまでは36度の三角比で出てきた内容の振り返りです。ここから、18度の三角比を求めていきます。点 B から CD に下した垂線の足を点 F とすると、18度を含む直角三角形が出てきます。辺の長さもわかるので、 $\sin 18^{\circ}$ は次のようになります。
\begin{eqnarray} \sin 18^{\circ} &=& \frac{\mathrm{ CF } }{\mathrm{ BC } } \\[5pt] &=& \frac{\mathrm{ AC }-\mathrm{ AD } }{2} \\[5pt] &=& \frac{\sqrt{5}-1}{4} \\ \end{eqnarray}

$\cos$ の値は、二重根号が出てきてしまいます。
\begin{eqnarray} \cos 18^{\circ} &=& \mathrm{ BF } \\[5pt] &=& \sqrt{ 1^2-\left(\frac{\sqrt{5}-1}{4}\right)^2 } \\[5pt] &=& \sqrt{ \frac{16-(5-2\sqrt{5}+1)}{16} } \\[5pt] &=& \sqrt{ \frac{10+2\sqrt{5} }{16} } \\[5pt] &=& \frac{ \sqrt{10+2\sqrt{5} } }{4} \\[5pt] \end{eqnarray} この二重根号はきれいに外せません。

$\tan$ も出せますが、直接出すよりも $72^{\circ}$ から考える方が楽なので、後で出しましょう。

72度の三角比

余角の公式を使うと、72度の三角比も出すことができます。\[ \sin 72^{\circ} = \frac{ \sqrt{10+2\sqrt{5} } }{4}, \ \cos 72^{\circ} = \frac{\sqrt{5}-1}{4} \]となります。

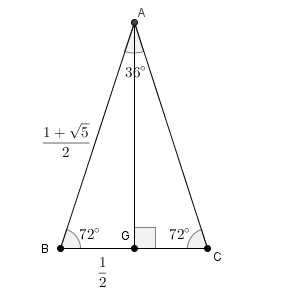
$\tan$ は、 A から BC に下した垂線の足を G とし、 $\triangle \mathrm{ ABG }$ で考えます。

\begin{eqnarray} \tan 72^{\circ} &=& \frac{\mathrm{ AG } }{\mathrm{ BG } } \\[5pt] &=& 2\sqrt{ \left(\frac{1+\sqrt{5} }{2}\right)^2-\left(\frac{1}{2}\right)^2 } \\[5pt] &=& \sqrt{ (6+2\sqrt{5})-1 } \\[5pt] &=& \sqrt{ 5 +2\sqrt{5} } \\ \end{eqnarray}となります。この結果を使えば、残っていた $\tan 18^{\circ}$ は余角の公式から、次のように計算できます。 \begin{eqnarray} \tan 18^{\circ} &=& \frac{1}{\tan 72^{\circ} } \\[5pt] &=& \frac{1}{\sqrt{ 5 +2\sqrt{5} } } \\[5pt] &=& \frac{\sqrt{ 5 -2\sqrt{5} } }{\sqrt{ 5 +2\sqrt{5} }\times\sqrt{ 5 -2\sqrt{5} } } \\[5pt] &=& \frac{\sqrt{ 5 -2\sqrt{5} } }{\sqrt{ 5^2 -(2\sqrt{5})^2 } } \\[5pt] &=& \frac{\sqrt{ 5 -2\sqrt{5} } }{\sqrt{ 5 } } \\[5pt] &=& \frac{\sqrt{ 25 -10\sqrt{5} } }{5 } \\ \end{eqnarray}となります。