【応用】ベクトルの終点の存在範囲（平行四辺形）

ここでは、ベクトルの終点の存在範囲を求める問題を見ていきます。答えが平行四辺形になるような例を取り上げます。

動く係数が1つの場合

図は次のようになっています。

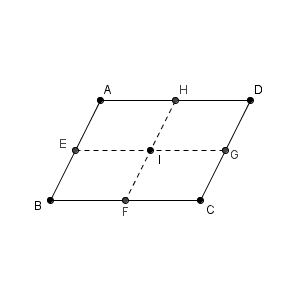
ベクトルの終点の存在範囲を求める問題は、【応用】ベクトルの終点の存在範囲（直線）でも考えました。リンク先のページでは、係数の和についての条件がありましたが、今回は、 $s,t$ の和に関する条件はありません。つまり、各係数は独立に動くことができます。この違いに注意して、順番に考えていきましょう。

まず、(1)は、 s だけが動きます。 $1\leqq s \leqq 2$ と動いたときに、 $s\overrightarrow{ \mathrm{ AE } }$ の終点がどうなるかを考えてみましょう。 s が変わると、ベクトルの長さが変わるだけですね。なので、 $s=1$ のときと $s=2$ のときを考えればいいです。終点はその間にきます。

$s=1$ のときは $s\overrightarrow{ \mathrm{ AE } }=\overrightarrow{ \mathrm{ AE } }$, $s=2$ のときは $s\overrightarrow{ \mathrm{ AE } }=\overrightarrow{ \mathrm{ AB } }$ となるので、 $s\overrightarrow{ \mathrm{ AE } }$ の終点は、線分 EB 上にあることがわかります。

これに $\overrightarrow{ \mathrm{ AH } }$ を足せばいいので、横にスライドさせればいいですね。よって、点 P の存在範囲は、「線分 IF 」となります。

2つの係数が独立に動く場合

続いて、「(2) $\overrightarrow{ \mathrm{ AP } }=s\overrightarrow{ \mathrm{ AE } }+t\overrightarrow{ \mathrm{ AH } }$, $1\leqq s \leqq 2$, $0\leqq t \leqq 1$ 」を考えましょう。

s, t の間に関係式はないので、両方が自由に動くことができます。なので、片方ずつ動かして考えましょう。

先ほど考えたように、 $s\overrightarrow{ \mathrm{ AE } }$ の終点は、線分 EB 上にあります。この線分上に点 J をとり、次に $\overrightarrow{ \mathrm{ AJ } }+t\overrightarrow{ \mathrm{ AH } }$ の終点を考えましょう。

t は $0\leqq t \leqq 1$ の値をとります。よって、 J を通り、 AH に平行な直線と FI との交点を K とすると、ベクトルの終点は線分 JK 上を動くことがわかります。

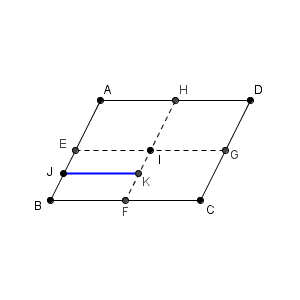
以上から、 s を動かし、各 s に対して t を動かすと考えれば、 P の存在範囲は、「平行四辺形 EBFI の周と内部」となることがわかります。

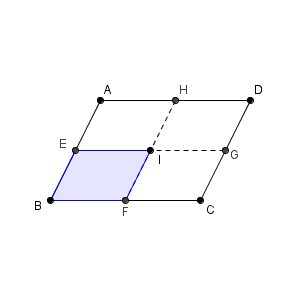
最後に、(3)を考えましょう。 $\overrightarrow{ \mathrm{ AP } }=s\overrightarrow{ \mathrm{ AE } }+(s+t)\overrightarrow{ \mathrm{ AH } }$, $0\leqq s \leqq 1$, $0\leqq t \leqq 1$ です。

$\overrightarrow{ \mathrm{ AH } }$ の係数がややこしくなっていますが、係数のややこしさをベクトルに押し付けてみましょう。
\begin{eqnarray} & & s\overrightarrow{ \mathrm{ AE } }+(s+t)\overrightarrow{ \mathrm{ AH } } \\[5pt] &=& s(\overrightarrow{ \mathrm{ AE } }+\overrightarrow{ \mathrm{ AH } })+t\overrightarrow{ \mathrm{ AH } } \\[5pt] &=& s\overrightarrow{ \mathrm{ AI } }+t\overrightarrow{ \mathrm{ AH } } \\[5pt] \end{eqnarray}となります。こうすれば、(2)と同じように考えることができます。答えは、「平行四辺形 AIGH の周と内部」となります。

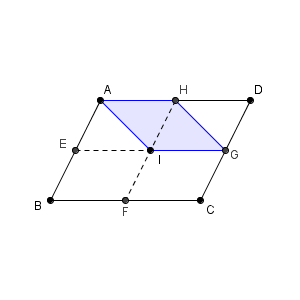
おわりに

ここでは、ベクトルの終点の存在範囲を求める問題を見ました。係数が独立に動くことで平行四辺形になるような例を取り上げました。独立に動ける場合は、片方ずつ動かして考えましょう。