【応用】「最小値の最大」問題は何をやっているか
今後、「最小値が最大になる場合」「最大値が最小になる場合」などを考える場面が出てきます。例えば、次のような問題です。
「最大値の最小」や「最小値の最大」というのは一体どういうことなのか、という話を別の例を使って説明したいと思います。
最高気温が最も低くなる日
「一日の最高気温が最も低くなる日」というのを考えてみましょう。一日の最高気温というのは、だいたいお昼過ぎの気温のことですよね。それが一番低くなるのが冬の日のどれかであることは、すぐにイメージすることができると思います。
少しくどいですが、このことをグラフを使って見てみましょう。一日の最高気温に関する次のグラフを見てください。
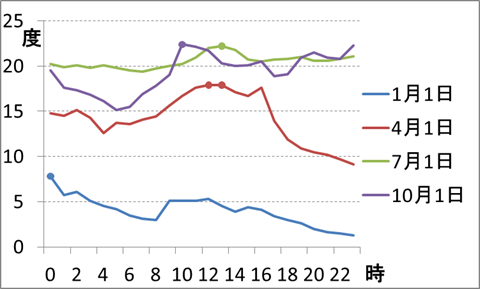
これは、東京都内の2015年の気温データ(気象庁のサイトをもとに作成)です。1月1日、4月1日、7月1日、10月1日の時間別の気温のデータのグラフで、1日の最高気温の時間帯に印をつけています。その日の天気にもよりますが、通常はお昼過ぎに最高気温になります。
続いて、2015年の「一日の最高気温」のグラフです。
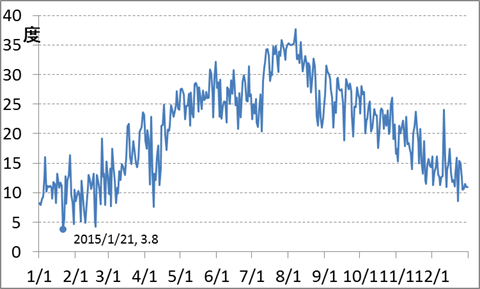
グラフから、最高気温が一番低かったのは、1月21日であったことがわかります。
「一日の最高気温が最も低くなる日」を考えるとき、考えている対象は3つあります。「時間」と「日」、そして「気温」です。「一日の最高気温」というのは、それぞれの「日」を固定して、「時間」を動かしたときの「気温」を考えているんですね。このとき、それぞれの日に対して、「最高気温」が決まります。
次に、その「最高気温」が低くなるときを考えます。この段階では、「日」を動かしたときの「最高気温」を考えることになります。動かしているものが変わっていることに注意します。「時間」はもう関係ありませんね。
順番としては、まず日を固定して時間と気温の関係を見る、次に日を動かして日と最高気温の関係を見る、となっています。
例題
ここでは問題は解かないのですが、どのような順番で問題を考えるか、ということだけ見てみます。
まずは、関数 $y=x^2-2ax+2a+1 \ (0\leqq x \leqq 2)$ の最小値を考えるんですね。 x を動かしたときに y が一番小さくなる時を求めます。
この前半部分は、【応用】二次関数の最大・最小(軸が動く)の例題(1)と同じなのですが、答えを見ると最小値は a の入った式になります。 a によって関数の最小値 m は変わるということです。これは「日によって最高気温が変わる」のと似ています。
m の最大値を求めるというのは、 a を動かしたときの m の最大値を求めるということです。これは、「日を動かして、最高気温が一番低くなる時を考える」のと似ています。
上で挙げた気温の例と、この例題との対応を書くと、次のようになります。
| 気温の例 | 例題 | |
|---|---|---|
| 動くもの | 時間、日、気温 | x, a, y |
| まず考えるもの | 時間と気温の関係 | x, y の関係 |
| 得られるもの | 各日の最高気温 | 各 a に応じた最小値m |
| 次に考えるもの | 日と最高気温の関係 | a, m の関係 |
考えるものや動かしているものが、前半と後半で変わっていることに注意しましょう。何を固定して、何を変化させているのか、というのを意識しながら考えないと、こんがらがって問題が解けなくなってしまいます。
おわりに
ここでは、「最大値の最小」や「最小値の最大」を考える前に、そもそもこれは何をやっているのか、という説明をしました。これを踏まえた二次関数での具体的な問題の解き方は、【応用】二次関数の最小値の最大で取り上げることとします。





