【応用】二変数二次関数の最大・最小（条件付）

ここでは $x, y$ という2つの変数が入った二次関数の最大・最小を考えます。ただし、2つの変数は自由に動くのではなくて、ある条件を満たしながら動くものを考えます。例題を見てみましょう。

例題

$x^2+2y^2$ には2つの変数が入っていますが、 $x+y=3$ という条件を使えば、1つの変数にすることができます。その結果、一変数二次関数の最小値を求める問題（よく見かける問題）になります。

条件から $y=3-x$ なので、
\begin{eqnarray} & & x^2+2y^2 \\ &=& x^2+2(3-x)^2 \\ &=& x^2+2x^2-12x+18 \\ &=& 3(x^2-4x)+18 \\ &=& 3(x-2)^2-12+18 \\ &=& 3(x-2)^2+6 \\ \end{eqnarray}$z=3(x-2)^2+6$ とおくと、このグラフは次のようになります。

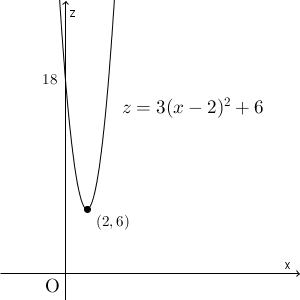
これから、 $x=2,y=1$ のときに最小値 $6$ をとることがわかります。

例題つづき

続いて、(2)をやってみましょう。

(1)で見たグラフの通り、定義域に何も制限がなければ $x^2+2y^2$ はどこまでも大きくなってしまいます。定義域に制限がついた場合で、この値の最大値を考えてみましょう。

$z=x^2+2y^2$ とおくと、(1)でみたとおり、\[ z=3(x-2)^2+6 \]となるんでしたね。 $x\geqq 0$ という条件があるので、この範囲でこの関数を考えればいい、…と考えたくなりますが、これは間違いです。

例えば、 $x=100$ とすると、 $x+y=3$ なので $y=-97$ となってしまい、 $y\geqq 0$ という条件を満たさなくなってしまいます。つまり、 x には他にも条件を考慮しないといけないことが分かります。

なぜこんなことが起こったのかというと、 $y=3-x$ と置いて y を消去した結果、 y の条件のことを忘れてしまったからなんですね。条件式を使って文字を消去するときには、その文字に関する条件も考慮しないといけないことに注意しましょう。

今の場合、 $y=3-x$ とおくときに、 $y\geqq 0$ の条件も x で書かないといけません。つまり、 $3-x\geqq 0$ だから $x\leqq 3$ という条件も考慮しないといけません。

あわせると、$0\leqq x \leqq 3$ の範囲で $z=3(x-2)^2+6$ の最大値を考える、ということになるわけです。グラフをかくと、次のようになります。

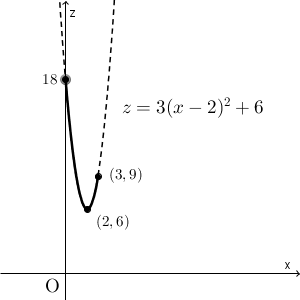
このことから、 $x=0,y=3$ のときに最大値 $18$ となることがわかります。

おわりに

y を x の式で置き換えるときは、 y の条件も x で置き換える、ということが大事です。これを忘れると、求めたいものとは別のものを求めてしまうことになります。

定義域がどうなるのかに注意すれば、他の部分は今まで見た通りの「定義域に制限があるときの二次関数の最大・最小を求める問題」になります。