🏠 Home / 数学C / ベクトル / 平面ベクトルの演算

【基本】ベクトル

🕒 2017/08/01 🔄 2024/07/09

ここでは、ベクトルとは何か、ベクトルが等しいとはどういうことか、を見ていきます。

📘 目次

ベクトルとは何か

座標を使って図形を考える場合、各頂点の座標や各直線の方程式を使って、図形をとらえていました。

これは、原点を基準とし、縦軸と横軸で世界を切り分けているわけですね。

ただ、この図形には初めから斜めの線しかないので、斜めを基準にしたほうが便利ではないか、という発想も出てきます（参考：【導入】ベクトルを考える意味について）。

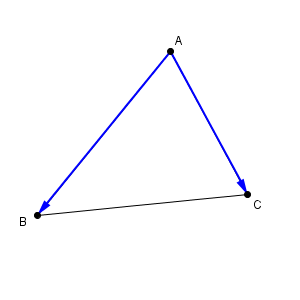
つまり、原点から見るのではなく、 A から見た B 、 A から見た C ととらえる、というわけです。 A を基準にして、そこからどの向きにどれほどの距離だけ離れているか、で他の点を表現するのですね。

この $\mathrm{A}$ から $\mathrm{B}$ というように、向きを考慮した線分のことを、有向線分といいます。A を始点、 B を終点といいます。

有向線分は、位置（どこにあるか）と向きと大きさで決まりますが、このうち、位置を問題にしないもの、つまり、向きと大きさで決まるものを、ベクトル(vector) と言います。上の図で、 A から B への向きと、線分 AB の長さを持つベクトルを\[ \overrightarrow{ \mathrm{ AB } } \]と表します。

同様に、 A から C への向きと、線分 AC の長さを持つベクトルは\[ \overrightarrow{ \mathrm{ AC } } \]と表します。

なお、 $\overrightarrow{ \mathrm{ AB } } = \vec{b}$ などとおいて、1つの文字でベクトルを表すこともあります。

ベクトルの大きさ

ベクトルは、向きと大きさを持つものなので、向き・大きさを表すものが欲しいですね。向きの表し方はまた後で見ることにして、ここではベクトルの大きさの表し方を見ます。

数字の場合、数字の大きさを表すものとして、絶対値がありました（参考：【基本】絶対値）。ベクトルの場合も、大きさを\[ | \overrightarrow{ \mathrm{ AB } } |, |\vec{a}| \]などと表します。なお、 $ \overrightarrow{ \mathrm{ AB } }$ の大きさ、つまり、$| \overrightarrow{ \mathrm{ AB } } |$ とは、線分 AB の長さのことです。

大きさが $1$ のベクトルは、単位ベクトル(unit vector) と呼ばれます。基本となる目盛りのようなものなので、これから時々出てきます。

ベクトルが等しいとは

ベクトルというのは、向きと大きさを持ったものです。なので、2つのベクトルの向きと大きさがそれぞれ同じであれば、その2つのベクトルは等しい、と考えます。位置が違っていてもかまいません。

例えば、次の図を見てみましょう。

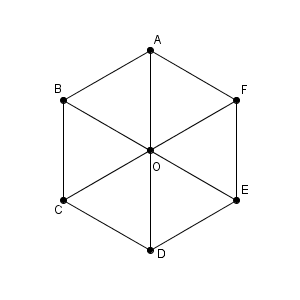
この六角形 ABCDEF は正六角形で、一番長い対角線の交点を O としたものです。このとき、 $\overrightarrow{ \mathrm{ AB } }$ と等しいベクトルはどれでしょうか。

向きが同じなら、線分 AB と平行になります。なので、直線 CF や直線 DE 上にあるベクトルが、候補となります。

それぞれの小さな三角形は正三角形なので、辺の長さは等しいです。このことから、 $\overrightarrow{ \mathrm{ AB } }$ と等しいベクトルは、 $\overrightarrow{ \mathrm{ FO } }$, $\overrightarrow{ \mathrm{ OC } }$, $\overrightarrow{ \mathrm{ ED } }$ であることがわかります。

なお、 $\overrightarrow{ \mathrm{ AB } }$ と $\overrightarrow{ \mathrm{ DE } }$ は、等しくありません。 AB と DE は長さが同じで平行ですが、この2つのベクトルは向きが反対です。向きが同じでなければ、ベクトルが等しいとはいえません。