【基本】正弦定理の基本的な使い方
ここでは、正弦定理の内容とその基本的な使い方を見ていきます。正弦定理の証明自体は別ページにあります。ここでは、正弦定理があればどんなことができるかを見ていきましょう。
なお、辺 $\mathrm{AB}$, $\mathrm{BC}$, $\mathrm{CA}$ の長さを、それぞれ、 $c,a,b$ と書き、角 $\angle \mathrm{ CAB }$, $\angle \mathrm{ ABC }$, $\angle \mathrm{ BCA }$ の大きさを、それぞれ、 $A,B,C$ と書くことにします。
この記事に関連する動画を公開しました。
正弦定理
正弦定理とは、このような内容です。
ちなみに、外接円とは、三角形の外側で接する円のことです。3つの頂点を通る円、ということもできます。
「辺の長さと角の大きさとの間にこういう関係式があるよ」という内容ですが、実際には、一部の辺の長さや角の大きさから他の辺や角を求めることに使います。例えば、正弦定理から、次の式が成り立つことが分かります。\[ a=\frac{b}{\sin B} \times \sin A \]これは、2つの角の大きさ(または $\sin$ )と1つの辺の長さが分かれば、他の辺の長さもわかるということを意味しています。具体的な使用例を見てみましょう。
例題1
正弦定理と見比べて、どのように求めるか考えてみましょう。
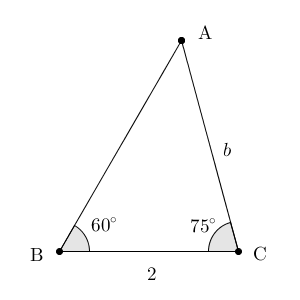
注意しなければいけないのは、辺と角の対応の仕方です。今求めたい b に対応する角(辺の向かいにある角)は $B=60^{\circ}$ です。一方、分かっている長さ a に対応する角は A です。これは与えられていませんが、他の2つの角度が分かっているので求められますね。\[ A=180^{\circ}-60^{\circ}-75^{\circ}=45^{\circ} \]これで、ようやく正弦定理が使えます。正弦定理より、 b は次のように計算できます。
\begin{eqnarray}
b
&=&
\frac{a}{\sin A} \times \sin B \\[5pt]
&=&
\frac{2}{\sin 45^{\circ} } \times \sin 60^{\circ} \\[5pt]
&=&
\frac{2}{\frac{\sqrt{2} }{2} } \times \frac{\sqrt{3} }{2} \\[5pt]
&=&
\sqrt{6}
\end{eqnarray}これが答えです。
途中で出てくる $\dfrac{2}{\frac{\sqrt{2} }{2} }$ のような式は初めて見るかもしれませんが、分子を分母で割っていると考えれば\[ \dfrac{2}{\frac{\sqrt{2} }{2} } = 2 \div \frac{\sqrt{2} }{2} \]を計算すればいいということがわかるでしょう。もしくは、分母と分子に $2$ をかけて\[ \dfrac{2}{\frac{\sqrt{2} }{2} } = \dfrac{2\cdot 2}{\frac{\sqrt{2} }{2} \cdot 2 }=\dfrac{4}{\sqrt{2}} \]と考えて計算することもできます。
なお、現時点では、 c を求めることはできません。 $\sin 75^{\circ}$ が求められないからです。【応用】15度の三角比で見た通り、現時点でも頑張れば求めることは可能ですが、普通は出題されません(将来学ぶ、三角関数以降の範囲では出題されます)。
裏ワザ的ですが、 $\sin$ が求められる角度の種類は少ないので、具体的な角度の大きさが出題されるパターンは限られる、とも言えます。
例題2
もう一問考えてみます。
先ほどと同じ三角形で、今度は外接円の半径を求めます。正弦定理より、次のようにして求めることができます。
\begin{eqnarray}
R
&=&
\frac{a}{2\sin A} \\[5pt]
&=&
\frac{2}{2\sin 45^{\circ} } \\[5pt]
&=&
\sqrt{2} \\[5pt]
\end{eqnarray}これが答えです。
これだけを見ると簡単そうに見えますが、実際にはこんな単純な出題のされ方はありません。図を見て、「この円はこの三角形の外接円になっている、だから正弦定理を使えば半径が求められる」などと自分で気づかなければいけない場面も出てきます。今後、いろんな問題を解きながら慣れていきましょう。
おわりに
ここでは、正弦定理の内容と基本的な使い方を見てきました。一部の辺の長さや角の大きさから他の辺や角を求めることができることを、例題を通じてみてきました。実際には図形と絡めて出題されることが多いのですが、問題を解きながら学んでいきましょう。





