【基本】ベクトルの引き算

🕒 2017/08/03 🔄 2024/07/09

ここでは、逆ベクトルやベクトルの引き算を見ていきます。

📘 目次

逆ベクトル

はじめての負の数の授業で、「 $2-3$ とは、 $2+(-3)$ とも言い換えられる」みたいな話が出てくることがあります。つまり、「引き算とは、負の数を足す」とも考えられる、ということです。

どうしてそんな回りくどい考え方をするのか、というツッコミもあるかと思いますが、ベクトルの引き算を考えるときにはこの考え方が役立ちます。

ベクトルの足し算の場合は、2つのベクトルをしりとりのようにくっつけて考えれば、足し算の定義は自然なものに感じられるでしょう（参考：【基本】ベクトルの足し算）。ただ、「ベクトルを引く」となると、そんなにイメージがつきやすいわけではありません。

しかし、「マイナスのベクトル」ならどうでしょうか。下の、 $\overrightarrow{ \mathrm{ AB } }$ に対し、 $-\overrightarrow{ \mathrm{ AB } }$ を定義するにはどうするのが自然でしょうか。

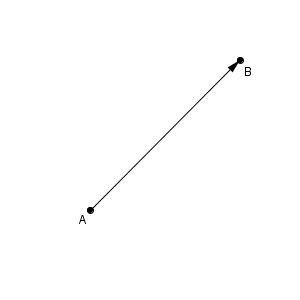
ベクトルは向きと大きさがあります。「マイナスの大きさ」は想像しにくいですが、「マイナスの向き」ならどうでしょう。「それって、反対向きってことじゃないか？」と考えるのが自然ですよね。

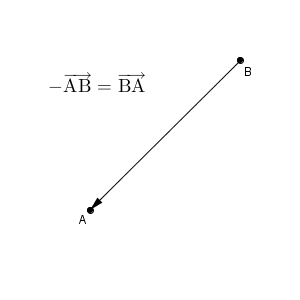
「マイナスのベクトルとは、元のベクトルを反対向きにしたもの」、式で書くと、\[ -\overrightarrow{ \mathrm{ AB } } = \overrightarrow{ \mathrm{ BA } } \]と考えるのが自然でしょう。

このように、あるベクトル $\overrightarrow{ \mathrm{ AB } }$ に対して、向きが反対で大きさが同じベクトルを、そのベクトルの逆ベクトル(opposite vector) といい、 $-\overrightarrow{ \mathrm{ AB } }$ で表します。向きが逆なので、これは $\overrightarrow{ \mathrm{ BA } }$ と等しいです。

ベクトルの引き算

ベクトルの引き算は、上で見た「逆ベクトル」を使って考えます。

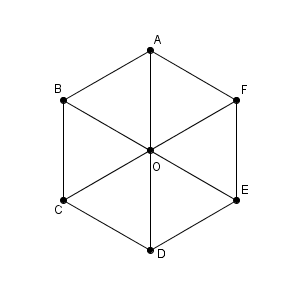
例えば、上のような正六角形があったとして、\[ \overrightarrow{ \mathrm{ OA } }-\overrightarrow{ \mathrm{ OB } } \]をどのように計算するかを考えてみましょう。これは、「 $\overrightarrow{ \mathrm{ OB } }$ を引く」ではなく、「 $-\overrightarrow{ \mathrm{ OB } }$ を足す」と考え、さらに「 $\overrightarrow{ \mathrm{ BO } }$ を足す」と考えます。逆ベクトルは、向きを反対にしたものですからね。

また、【基本】ベクトルの足し算の平行四辺形を用いた方法からすぐにわかる通り、足す順番を変えても結果が変わらないことをあわせて使えば、
\begin{eqnarray} \overrightarrow{ \mathrm{ OA } }-\overrightarrow{ \mathrm{ OB } } &=& \overrightarrow{ \mathrm{ OA } }+\overrightarrow{ \mathrm{ BO } } \\ &=& \overrightarrow{ \mathrm{ BO } }+\overrightarrow{ \mathrm{ OA } } \\ &=& \overrightarrow{ \mathrm{ BA } } \end{eqnarray}となります。

また、そもそも
\begin{eqnarray} \overrightarrow{ \mathrm{ OB } }+\overrightarrow{ \mathrm{ BA } }=\overrightarrow{ \mathrm{ OA } } \end{eqnarray}となることからも、上の引き算の決め方が自然であることがわかります。

なお、教科書によっては、「 $\overrightarrow{ \mathrm{ OB } }+\overrightarrow{ \mathrm{ BA } }=\overrightarrow{ \mathrm{ OA } }$ が成り立つから、これを利用して $\overrightarrow{ \mathrm{ OB } }$ を引くことを $\overrightarrow{ \mathrm{ OA } }-\overrightarrow{ \mathrm{ OB } }=\overrightarrow{ \mathrm{ BA } }$ で定める」としているものもあります。ここでは逆ベクトルを使って定めましたが、どちらでも同じ内容になりますし、逆ベクトルを使って考えたほうがわかりやすいと思うので、こちらを採用しています。