【基本】ベクトルの定数倍
ここでは、ベクトルを2倍したり、-1倍したりする方法、ベクトルの定数倍について見ていきます。
ベクトルの定数倍
次のような正六角形について考えてみましょう。
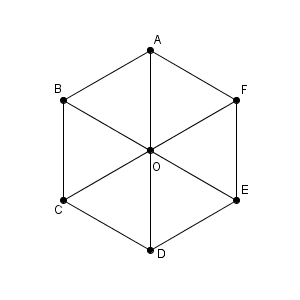
このとき、 $\overrightarrow{ \mathrm{ OA } }=\vec{a}$ としましょう。そうすると、 $\overrightarrow{ \mathrm{ CB } }$ や $\overrightarrow{ \mathrm{ EF } }$ も $\vec{a}$ となります。向きと大きさが同じですからね。 $\overrightarrow{ \mathrm{ DO } }$ も $\vec{a}$ です。
ここで、 $\overrightarrow{ \mathrm{ DA } }$ について考えてみましょう。これは、 $\overrightarrow{ \mathrm{ DO } }+\overrightarrow{ \mathrm{ OA } }$ と等しいですね。ただ、どちらも $\vec{a}$ なので、 $\vec{a}+\vec{a}$ となります。これを $2\vec{a}$ と書くことは自然でしょう。同じ向きで長さが2倍なのだから、こう書くことに違和感を覚える人は少ないはずです。
また、 $\overrightarrow{ \mathrm{ AD } }$ は、
\begin{eqnarray}
\overrightarrow{ \mathrm{ AO } }+\overrightarrow{ \mathrm{ OD } }
&=&
-\overrightarrow{ \mathrm{ OA } }-\overrightarrow{ \mathrm{ DO } } \\
&=&
-\vec{a}-\vec{a}
\end{eqnarray}となります。先ほどと向きが反対になったのだから、これを $-2\vec{a}$ と書くのも自然ですね。
以上のことを踏まえて、ベクトルの定数倍を次のように定義します。
定数 k とベクトル $\vec{a}(\ne\vec{0})$ があったとします。
- $k\gt 0$ のときは、 $\vec{a}$ と同じ向きで、長さが k 倍のベクトルを $k\vec{a}$ とします。
- $k\lt 0$ のときは、 $\vec{a}$ と反対の向きで、長さが $|k|$ 倍のベクトルを $k\vec{a}$ とします。
- $k=0$ のときは、 $k\vec{a}=\vec{0}$ とします。
また、 $\vec{a}=\vec{0}$ のときは、 $k\vec{0}=\vec{0}$ とします。
このようにして、 $k\vec{a}$ を決めます。「長さを $|k|$ 倍にして、向きは正負に応じて決める」という決め方です。この定義に、そんなに引っかかる人はいないでしょう。
1つ注意点としては、「ベクトルとベクトルを掛けているわけではない」ということです。ここで定義しているのは、「数とベクトルの積」です。ベクトルには向きがあるので、「2つのベクトルを掛ける」のと「数とベクトルを掛ける」のとでは、話が違ってきます。これについては、また別の機会に取り上げます。
なお、ベクトルに対して、ベクトルに掛けることのできる数のことを、スカラー(scalar) と呼ぶことがあります。
特殊な数を掛ける場合
特殊な数を掛けた場合を考えてみましょう。
まず、上でも出てきましたが、 $0$ を掛ける場合。これは、長さが $0$ になるのだから、 $\vec{0}$ となります。\[ 0\vec{a}=\vec{0} \]これが、どんなベクトル $\vec{a}$ についても成り立ちます。
また、 $1$ を掛ける場合。これは、長さが $1$ 倍で向きが同じベクトルになるので、元のベクトルそのものですね。\[ 1\vec{a}=\vec{a} \]となります。
次に、 $-1$ を掛ける場合。これは、長さが $|-1|=1$ 倍で、向きが反対のベクトルになるので、逆ベクトルですね。\[ (-1)\vec{a}=-\vec{a} \]細かい話をすると、左辺は $\vec{a}$ を $-1$ 倍したベクトル、右辺は逆ベクトルです。表現の仕方は違いますが、同じものを表します。
最後に、 $-k$ を掛ける場合について考えてみましょう。 $k\ne 0$ のときは、 $(-k)\vec{a}$ というのは、 長さが $|k|$ 倍のベクトルです。 $(-k)\vec{a}$ の向きは、 $k\gt 0$ のときは $\vec{a}$ と逆、 $k\lt 0$ のときは $\vec{a}$ と同じです。よって、 $(-k)\vec{a}$ は $k\vec{a}$ の逆ベクトルです。よって、\[ (-k)\vec{a}=-k\vec{a} \]が成り立ちます。 $k=0$ のときは、両辺が $\vec{0}$ となるので、成り立ちますね。
結果だけを見ると当たり前に思えますが、定義したものと示すものをよく区別していないと混乱してしまうので注意が必要です。
おわりに
ここでは、ベクトルの定数倍について見ました。正の数を掛けるなら同じ向きに長さを伸ばし、負の数を掛けるなら反対向きに長さを伸ばす、ということをおさえておきましょう。





