【基本】内分点と外分点の位置ベクトル
ここでは、位置ベクトルの理解を深めるため、内分点と外分点の位置ベクトルについて見ていきます。
内分点と外分点の復習
内分点・外分点は、線分をある比で分ける点のことです。【基本】平面上での内分点と外分点などで扱っています。
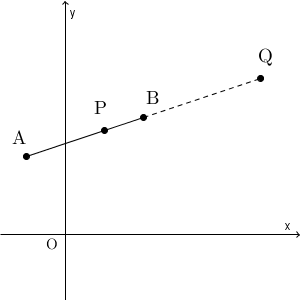
例えば、線分 AB を $m:n$ に内分する点を P とすると、 P は線分 AB 上の点で\[ \mathrm{ AP }:\mathrm{ PB }=m:n \]を満たすということです。
また、点 Q が線分 AB を $m:n$ に外分する点である、というのは、 Q は線分 AB の延長線上にある点で\[ \mathrm{ AQ }:\mathrm{ QB }=m:n \]を満たすということです。 $m\gt n$ なら、上の図のように、点 Q は線分 AB の B 側の延長線上にあり、 $m\lt n$ なら、点 Q は A 側の延長線上にあります。
比が線分の長さを表しています。内分点も外分点も直線上にありますが、線分上にあるのが内分点、ないのが外分点です。線分の内側か外側か、に対応させて考えると覚えやすいです。
内分点と外分点の位置ベクトル
さて、2点 A, B を結んでできる線分 AB を、 $m:n$ に内分する点について考えましょう。これらを位置ベクトルを使ってどう表されるかを見ていきます。
まず、 A, B の位置ベクトルを、それぞれ $\vec{a}$, $\vec{b}$ とします。また、点 P の位置ベクトルを $\vec{p}$ とします。
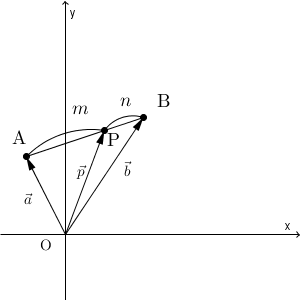
続いて、外分点の位置ベクトルを求めましょう。
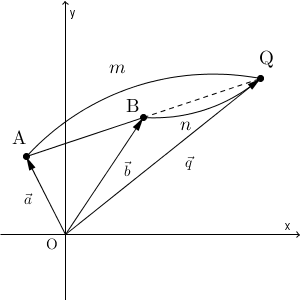
$m\gt n$ とします。大きさによって、点の位置が A 側か B 側かが変わるため、どちらが大きいかを仮定します。ただ、逆の場合も同じように考えればOKです。
このとき、 AB と AQ の長さの比が $(m-n):m$ となっているため、
\begin{eqnarray}
\overrightarrow{ \mathrm{ OQ } }
&=&
\overrightarrow{ \mathrm{ OA } }+\overrightarrow{ \mathrm{ AQ } } \\[5pt]
&=&
\overrightarrow{ \mathrm{ OA } }+\frac{m}{m-n}\overrightarrow{ \mathrm{ AB } } \\[5pt]
\end{eqnarray}となります。よって、 Q の位置ベクトル $\vec{q}$ は
\begin{eqnarray}
\vec{q}
&=&
\vec{a}+\frac{m}{m-n}(\vec{b}-\vec{a}) \\[5pt]
&=&
\frac{(m-n-m)\vec{a}+m\vec{b} }{m-n} \\[5pt]
&=&
\frac{-n\vec{a}+m\vec{b} }{m-n} \\[5pt]
\end{eqnarray}となります。先ほどの内分点の式で、 $n$ を $-n$ に置き換えたものになっています。
まとめると、次のようになります。
\[ \vec{p}=\frac{n\vec{a}+m\vec{b} }{m+n},\ \vec{q}=\frac{-n\vec{a}+m\vec{b} }{m-n} \]
例えば、2点 $\mathrm{ A }(\vec{a})$, $\mathrm{ B }(\vec{b})$ を結んでできる線分 AB を $2:1$ に内分する点の位置ベクトルは $\dfrac{\vec{a}+2\vec{b} }{3}$ となり、 $2:1$ に外分する点の位置ベクトルは $-\vec{a}+2\vec{b}$ となります。
【基本】平面上での内分点と外分点で得られた式と見比べてみましょう。よく似た式になっていることがわかります。
おわりに
ここでは、内分点と外分点の位置ベクトルについて見てきました。座標で考えたときと似た式が得られます。結果は、一見すると複雑ですが、比の外側同士・内側同士の積と対応させることができるので、それほど覚えにくくはないでしょう。





